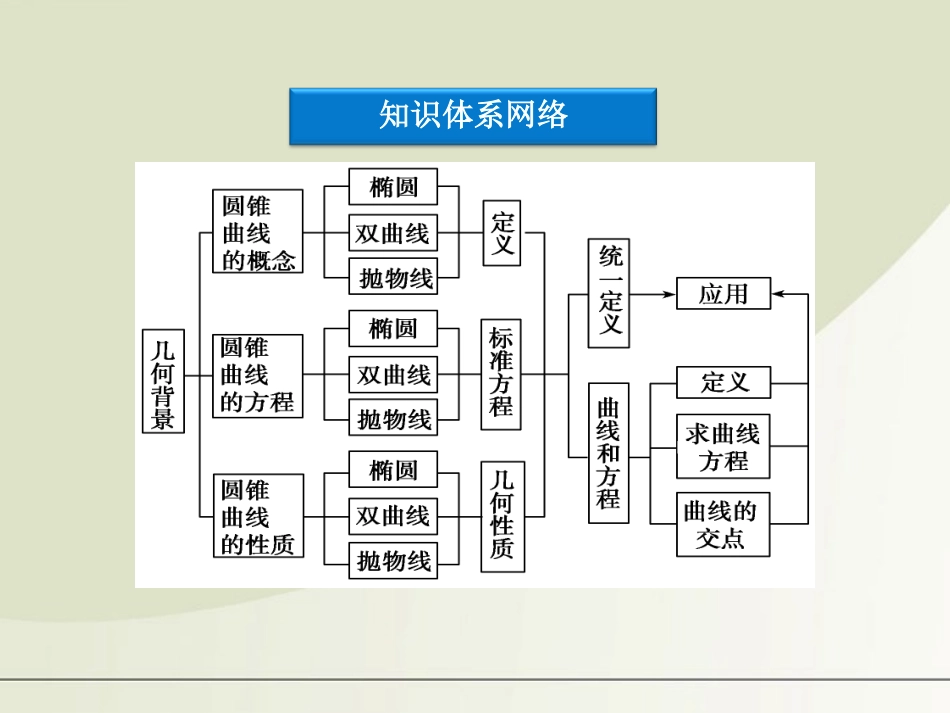
本章优化总结专题探究精讲章末综合检测本章优化总结知识体系网络知识体系网络专题探究精讲圆锥曲线的定义(1)椭圆的定义中,平面内动点与两焦点F1、F2的距离之和大于F1F2这一条件不可忽视.若这个距离之和小于F1F2,则这个动点轨迹不存在;若距离之和等于F1F2,则动点轨迹是线段F1F2.(2)双曲线的定义中,要注意条件2aF1F2,则无轨迹.双曲线定义中,M是双曲线上一点,若MF1MF2,则动点M的轨迹又为另一支,而双曲线是由两个分支组成的,故在定义中应为“差的绝对值”.(3)抛物线定义中,条件“点F不在直线l上”不能忽视,否则轨迹是过F且与直线l垂直的直线,而不是抛物线.已知A(0,7),B(0,-7),C(12,2),以C为一个焦点作过A、B的椭圆,求椭圆的另一个焦点F的轨迹方程.【思路点拨】依据椭圆的定义,列出关系式,再将其坐标化即可.例1【解】|AC|=13,|BC|=15,|AB|=14.又|AF|+|AC|=|BF|+|BC|,∴|AF|-|BF|=|BC|-|AC|=2,故F点的轨迹是以A,B为焦点,实轴长为2的双曲线,又c=7,a=1,b2=48,∴F点的轨迹方程是y2-x248=1(y≤-1).【名师点评】题目中的条件通过变形转化,结合圆锥曲线的定义等判断曲线类型,再求其轨迹方程.求圆锥曲线的标准方程通常有下列两种方法:(1)定义法,(2)待定系数法.求圆锥曲线的标准方程椭圆中的四个主要元素a,b,c,e中有a2=b2+c2,e=ca两个关系,因此确定椭圆标准方程只需两个独立条件.双曲线的四个主要元素a,b,c,e中有c2=a2+b2,e=ca两个关系,因此确定双曲线标准方程也只需两个独立条件.需要注意的是:无论哪种方法,都要分清楚焦点在x轴上还是y轴上,还是都有可能.已知圆C:(x+1)2+y2=25及点A(1,0),Q为圆上任一点,AQ的垂直平分线交CQ于M,求点M的轨迹方程.【思路点拨】由点M在线段AQ的垂直平分线上知MQ=MA,又QC=QM+MC,由此可转化为MC+MA=R(定值),结合椭圆定义求解.例2【解】如图所示, M是AQ的垂直平分线与CQ的交点,连结MA,∴MQ=MA. MC+MA=MC+QM=QC=5,又AC=2,∴点M的轨迹是以A、C为焦点的椭圆,且2a=5,2c=2.∴a=52,c=1.∴b2=a2-c2=254-1=214.【名师点评】求解本题主要利用了线段垂直平分线的性质将问题转化为动点M到两定点距离之和为常数,从而利用椭圆定义求出a,b∴点M的轨迹方程为x2254+y2214=1.与圆锥曲线有关的最值问题的求解策略与方法.(1)平面几何法涉及到最值问题的几何意义主要有三个:两点间的任意折线段长之和,以两点间直线段长为最短.|AB-AC|≤BC,当且仅当A、B、C三点共线,且A在B、C外侧时取“=”.圆锥曲线中的最值问题(2)目标函数法建立目标函数与圆锥曲线有关的最值问题,是常规方法,关键是选取适当的变量建立目标函数,然后运用求函数最值的方法确定最值.(3)判别式法主要是由条件得到一个相关的一元二次方程,该方程有解必须满足Δ≥0,从而得到某个不等式.已知点A(4,-2),F为抛物线y2=8x的焦点,点M在抛物线上移动,当|MA|+|MF|取最小值时,点M的坐标为________.例3【解析】如图,过点M作准线l的垂线,垂足为E,由抛物线定义知|MF|=|ME|,当点M在抛物线上移动时,|ME|+|MA|的值在变化,显然当M移到M′时,A、M′、E共线,|M′E|+|M′A|最小,此时AM′∥Ox,把y=-2代入y2=8x,得x=12,所以M′12,-2.【名师点评】本题求最值是利用抛物线的定义进行转化,结合平面知识求最值.【答案】12,-2判断直线l与圆锥曲线C的位置关系时,可将直线l的方程代入曲线C的方程,消去y(或x)得一个关于变量x(或y)的一元二次方程ax2+bx+c=0.当a≠0时,若Δ>0,则直线l与曲线C相交;若Δ=0,则直线l与曲线C相切;若Δ<0,则直线l与曲线C相离.直线与圆锥曲线的位置关系当a=0时,即得到一个一次方程,则l与C相交,且只有一个交点.此时,若C为双曲线,则l平行于双曲线的渐近线;若C为抛物线,则l平行于抛物线的对称轴.1.中点弦问题过...