余弦定理约课时VIP免费

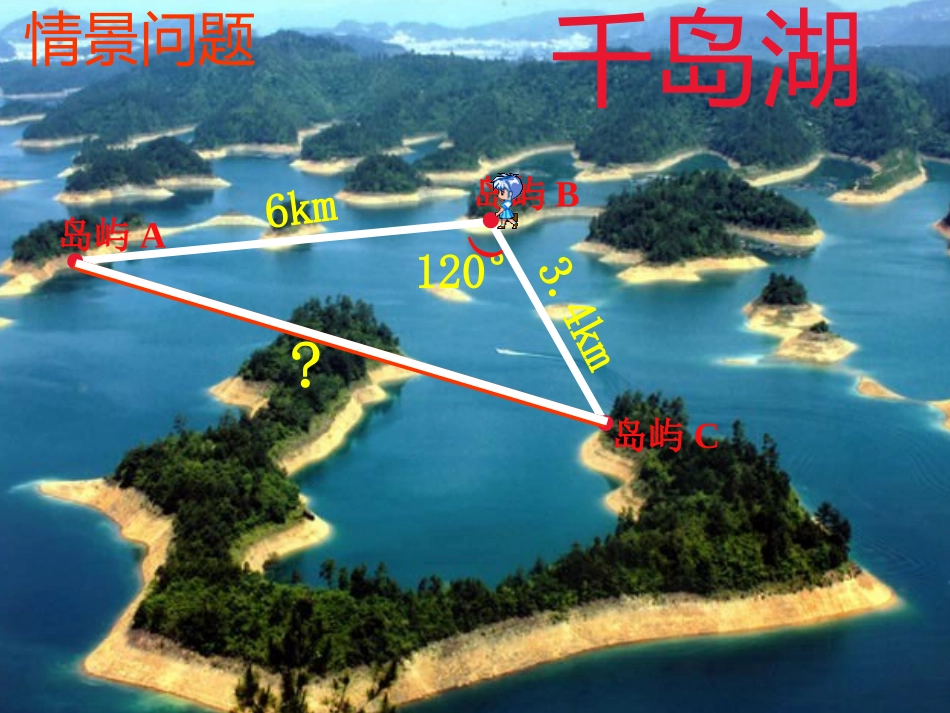
主备人：罗瑜唐强审核人：牟必继1.1.2余弦定理书山有路勤为径，学海无涯苦作舟。千岛湖3.4km6km120°）情景问题岛屿B岛屿A岛屿C?千岛湖千岛湖情景问题3.4km6km120°）岛屿B岛屿A岛屿C?3.4km6km120°ABC在△ABC中，已知AB=6km，BC=3.4km，∠B=120o，求AC用正弦定理能否直接求出AC？）1.1.2余弦定理CBAcab探究：在△ABC中，已知CB=a,CA=b，CB与CA的夹角为∠C，求边c.﹚cABbCAaCB,,设)()(babaccc2babbaa2Cabbacos222Cabbaccos2222由向量减法的三角形法则得Cbabacos222bacCBAcab﹚Abccbacos2222﹚)()(babaccc2babbaa2Cabbacos222Cabbaccos2222由向量减法的三角形法则得Cbabacos222bac探究△：若ABC为任意三角形，已知角C，BC=a,CA=b,求AB边c.cABbCAaCB,,设CBAcab﹚Baccabcos2222余弦定理Abccbacos2222)()(babaccc2babbaa2Cabbacos222Cabbaccos2222由向量减法的三角形法则得Cbabacos222探究△：若ABC为任意三角形，已知角C，BC=a,CA=b,求AB边c.cABbCAaCB,,设bac（向量法证明）Cabbaccos2222Abccbacos2222Baccabcos2222一.余弦定理三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。CBAbac对余弦定理还有其他证明方法吗?C点的坐标为()AbAbsin,cosxyB(c,0)Cbc如图，以点A为原点，边AB所在直线为x轴建立直角坐标系A)sin,cos(AbAba(0,0)由两点距离公式知：AcbbcaaBCAbAbcBCcos2)sin0()cos(22222（坐标法证明）二.余弦定理的推论三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。CBAbacCabbaccos2222Abccbacos2222Baccabcos2222bcacbA2cos222acbcaB2222cosabcbaC2cos222推论：利用余弦定理可以解决什么类型的三角形问题？三、利用余弦定理，可以解决以下两类有关三角形的问题：（1）已知两边和它们的夹角，求第三边和其他两个角；（2）已知三边，求三个角。（1）若A为直角，则a²=b²+c²（2）若A为锐角，则a²b²+c²由a2=b2+c2－2bccosA可得CcBAbaCabCba由上可知，余弦定理可以看作是勾股定理的推广。3.4km6km120°）ABC例1、△在ABC中，已知AB=6km，BC=3.4km，∠B=120o，求AC四.定理的应用定理的应用解：由余弦定理得答：岛屿A与岛屿C的距离为8.24km.BBCABBCABACcos222296.67120cos4.3624.3622o24.8AC例2.已知b=8,c=3,A=600求a.∵a2=b2+c2－2bccosA=64+9－2×8×3cos600=49解：a=7变式练习：1.已知:a=7,b=8,c=3,求A.2.已知:a=7,b=8,c=3,试判断此三角形的形状.例3：在⊿ABC中，已知b=60cm,c=34cm,A=41°,解三角形（角度精确到1°，边长精确到1cm）.解：根据余弦定理，a²=b²+c²－2bccosA=60²+34²－2×60×34×cos41°≈1676.82所以a≈41(cm)由正弦定理得，.5440.041656.0344141sin34sinsinaAcC因为c不是三角形中最大的边，所以C是锐角，利用计算器得C≈33°B=180°－（A+C）=180°－（41°＋33°）＝106°例4，在⊿ABC中，已知a=134.6cm,b=87.8cm,c=161.7cm,解三角形（角度精确到1′）解：由余弦定理的推论得：,5543.07.1618.8726.1347.1618.872cos222222bcacbAA≈56°20′;,8398.07.1616.13428.877.1616.1342cos222222cabacBB≈32°53′C=180°－（A+B）≈180°－（56°20′＋32°53′）＝90°47′五.四类解三角形问题：（1）已知两角和任意一边，求其他两边和一角；（2）已知两边和其中一边的对角，求其他的边和角。（3）已知两边和它们的夹角，求第三边和其他两个角；（4）已知三边，求三个角。2.若A,B,C是⊿ABC的三个内角，则sinA+sinB____sinC.)(sin3sin,2.3等于则中，在BBBCABCA.b/aB.a/bC.a/cD.c/a1.若三角形的三个角的比是1：2：3，最大的边是20，则最小的边是_____.六.课堂练习：4△、在ABC中,若a=4、b=5、c=6，△判断ABC的形状.ADCB)300)4505、如图所示，已知BD=3，DC=5∠，B=300∠，ADC=450，求AC的长。七.回顾与小结:222cos2bcaAbc222cos2cabBca222cos2abcCab3.余弦定理可以解决的有关三角形的问题：（1）已知两边及其夹角，求第三边和其他两个角。（2）已知三边求三个角；（3）判断三角形的形状Cabbaccos2222Abccbacos2222Baccabcos22221.余弦定理：2.推论:八.作业:P10A组3，4题