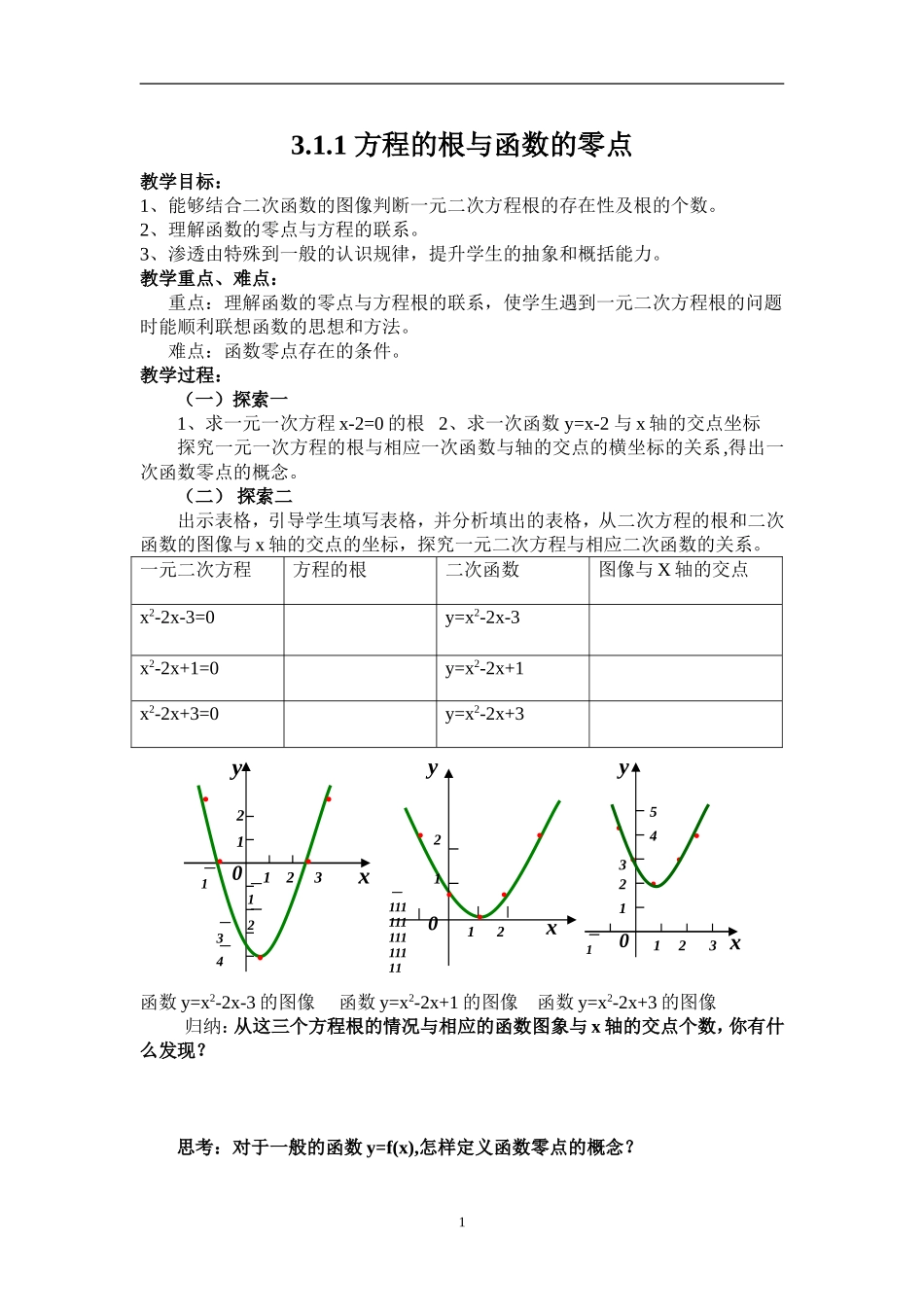
3.1.1方程的根与函数的零点教学目标:1、能够结合二次函数的图像判断一元二次方程根的存在性及根的个数。2、理解函数的零点与方程的联系。3、渗透由特殊到一般的认识规律,提升学生的抽象和概括能力。教学重点、难点:重点:理解函数的零点与方程根的联系,使学生遇到一元二次方程根的问题时能顺利联想函数的思想和方法。难点:函数零点存在的条件。教学过程:(一)探索一1、求一元一次方程x-2=0的根2、求一次函数y=x-2与x轴的交点坐标探究一元一次方程的根与相应一次函数与轴的交点的横坐标的关系,得出一次函数零点的概念。(二)探索二出示表格,引导学生填写表格,并分析填出的表格,从二次方程的根和二次函数的图像与x轴的交点的坐标,探究一元二次方程与相应二次函数的关系。一元二次方程方程的根二次函数图像与X轴的交点x2-2x-3=0y=x2-2x-3x2-2x+1=0y=x2-2x+1x2-2x+3=0y=x2-2x+3函数y=x2-2x-3的图像函数y=x2-2x+1的图像函数y=x2-2x+3的图像归纳:从这三个方程根的情况与相应的函数图象与x轴的交点个数,你有什么发现?思考:对于一般的函数y=f(x),怎样定义函数零点的概念?xy0-132112-1-2-3-4.....yx0-111111111111112112..........xy0-1321125431应用一1、如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是()Am>–2Bm<–2Cm>2Dm<22、函数f(x)=x3-16x的零点为()A(0,0),(4,0)B0,4C(–4,0),(0,0),(4,0)D–4,0,4通过应用一总结:怎样求函数的零点?(三)探索三观察图象,完成以下填空:(Ⅰ)二次函数y=x2-2x-3①f(-2)0,f(1)0,f(-2)·f(1)0f(2)0,f(4)0,f(2)·f(4)0(填“>”、“<”)发现在区间(-2,1)和(2,4)上____零点(填“有”或“无”)②f(2)·f(1)0,(填“>”、“<”)发现在区间(2,4)上____零点(填“有”或“无”)(Ⅱ)函数y=f(x)的图象如下:由图可知f(m)_0,f(n)_0,f(m)·f(n)0f(p)0,f(q)0,f(p)·f(q)0(填“>”、“<”)发现在区间(m,n)(p,q)上____(填“有”或“无”)由以上两步探索,你可以得出什么样的结论(尝试口头表达)?结论:零点存在定理思考:对于连续不断的曲线函数,是否满足f(a)·f(b)<0就一定有零点存在,如果满足f(a)·f(b)>0,是否一定没有函数零点存在,满足条件的零点个数是否是唯一的?应用二1、对于定义在R上的函数y=f(x),若f(a)·f(b)<0(a,b∈R,且a