函数的定义域VIP免费

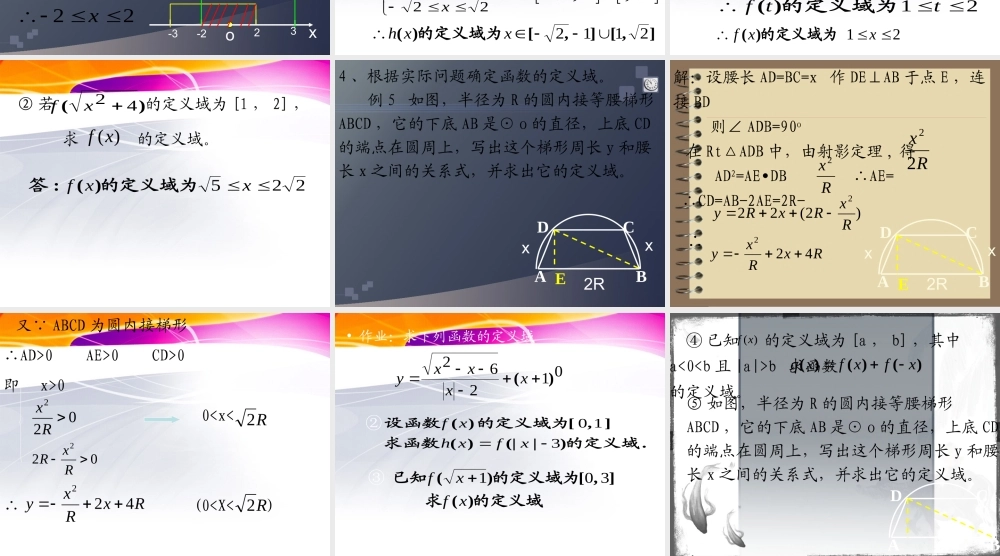
函数定义域的求法 1 、根据解析式求定义域例 1 求下列函数的定义域 02)1(412xxxxy① 012201x0-4|x|xx:解14 43 4xxxxx且或),(],(),(),(:431144 x原函数的定义域为 2112xxy②2211 02012xxxxxx或或,||.,的取值范围求为一切实数定义域的若函数aaxaxy 862③2 2xx或 ]4[)(4)0( 2)4( 422）（）定义域为：（则）已知函数（ffxfxfxxxx 2 、已知 的定义域，求 的定义域。例 2: )(xf))((xf .)()()(的解析式试求若已知xhxfxxf 12h(x) 12 ①xxxhxxf424 121212)())(（答： ② 已知 的定义域为 [-3 ， 2] ， 求函数 的定义域。)(xf)()()(xfxfxg2323 23 xxxgxxf定义域为定义域为解)(],[)(: xo-3-2233223xx22x 1120 10 10 12 xtxxfxt即的定义域为设解)(: ③ 设函数 的定义域为 [0 ， 1] ，求函数 的定义域。)(xf)()(12 xfxH 21122211221,,xxxxx或],[],[)(2112xxh的定义域为 3 、已知 的定义域，求 的定义域。 例 3 ① 已知 定义域为 [0 ， 3] ，求 的定义域。 )(xf )(xf)1(xf)(xf 21 21 30 1 ttftxxt的定义域为设解)(:21 xxf的定义域为)( ② 若 的定义域为 [1 ， 2] ， 求 的定义域。)(42 xf)(xf225xxf的定义域为答)(: 4 、根据实际问题确定函数的定义域。 例 5 如图，半径为 R 的圆内接等腰梯形ABCD ，它的下底 AB 是⊙ o 的直径，上底 CD的端点在圆周上，写出这个梯形周长 y 和腰长 x 之间的关系式，并求出它的定义域。ABCDExx2R 解：设腰长 AD=BC=x 作 DE⊥AB 于点 E ，连接 BD 则∠ ADB=90o 在 Rt△ADB 中，由射影定理 , 得 AD2=AE DB ∴AE= • ∴CD=AB-2AE=2R- ∴ Rx22Rx 2)2(222RxRxRyRxRxy422ABCDExx2R 又∵ ABCD 为圆内接梯形 ∴AD>0 AE>0 CD>0即 x>0 0b 求函数 的定义域。)(xf)()()(xfxfxg⑤ 如图，半径为 R 的圆内接等腰梯形ABCD ，它的下底 AB 是⊙ o 的直径，上底 CD的端点在圆周上，写出这个梯形周长 y 和腰长 x 之间的关系式，并求出它的定义域。ABCD