二次根式的加减法VIP专享VIP免费

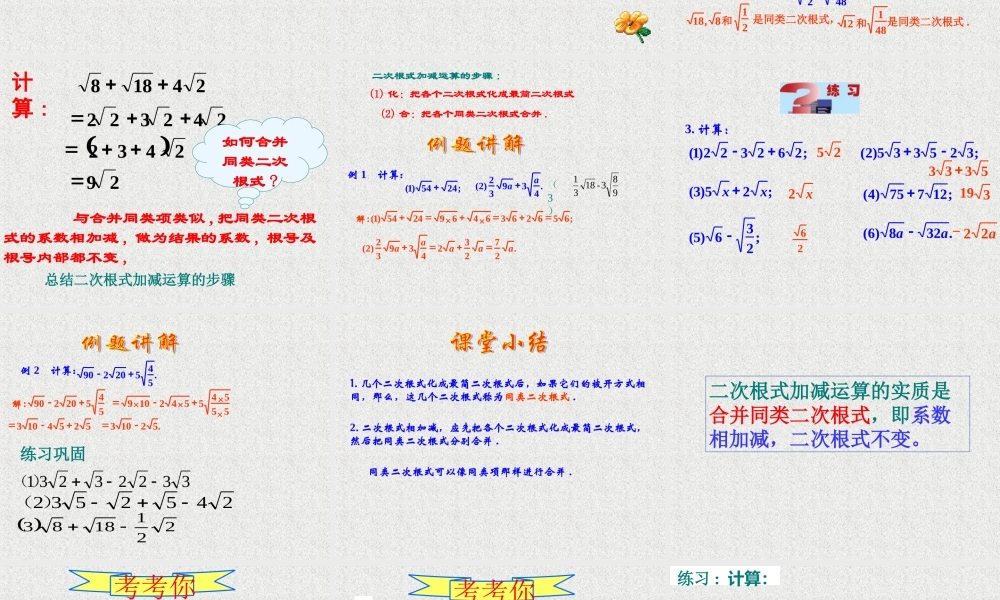
化简下列二次根式 _____;12 _____48 ______;50______;8_______;18_____;21_____;45 ________34 32342225222353332复习复习 2 、什么是同类项？ 所含字母相同，并且相同字母的指数也相同的项，叫做同类项3 、怎样合并同类项。温故知新温故知新3233= ？如何计算 呢？如何计算 呢？484273 35)6(32)5(188)4(818)3(553)2(535)1( 5452252计算计算 ::有什么发现？有什么发现？ 同类二次根式 : 几个二次根式化成 ___________ 以后，如果 _______ 相同，这几个二次根式就叫做同类二次根式 。最简二次根式被开方数 484273 344333 31639== （ 9+16 ） 3 =25 3 1 、判断下列各组二次根式是否为同类二次根式 ? （ 1 ） （ ） （ 2 ） （ ） （ 3 ） （ ） 5.050与1812与aa13与是否是 A.① 和②B.② 和③C.① 和③ D.③ 和④ 1. 以下二次根式：, ②12222327 , ④, ③①中，与3是同类二次根式的是（ ） .2. 下列二次根式中，哪些是同类二次根式？481,21,8,12,18,18和821 是同类二次根式， 12 和 481 是同类二次根式 .C 与合并同类项类似 , 把同类二次根式的系数相加减 , 做为结果的系数 , 根号及根号内部都不变 ,29 243224232224188总结二次根式加减运算的步骤计算 :如何合并同类二次根式 ? (1) 化：把各个二次根式化成最简二次根式 (2) 合：把各个同类二次根式合并 .例 1 计算：;2454)1(.43932)2(aa ;65626364692454)1(:××解.2723243932)2(aaaaa 983-1831（3）二次根式加减运算的步骤 : 3. 计算：;262322)1(;325335)2(;25)3(xx ;12775)4(;236)5(.328)6(aa 2553332 x31926a22- 例 2 计算：.54520290.52103525410354520290:解55545542109××××33223231）（2452532）（ 2211883练习巩固 1. 几个二次根式化成最简二次根式后，如果它们的被开方式相同，那么，这几个二次根式称为同类二次根式 .2. 二次根式相加减，应先把各个二次根式化成最简二次根式，然后把同类二次根式分别合并 .同类二次根式可以像同类项那样进行合并 . 二次根式加减运算的实质是合并同类二次根式，即系数相加减，二次根式不变。 1. 在下列各组根式中，是同类二次根式的是（ ）A . B . C....