《平面向量的基本定理》课件（新人教A版必修4）VIP免费

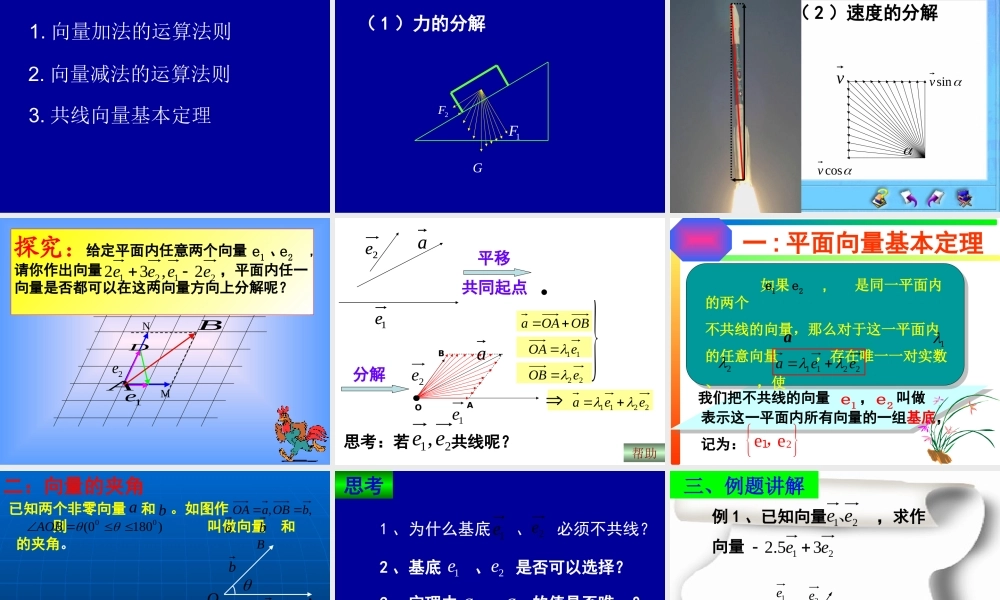
1. 向量加法的运算法则3. 共线向量基本定理复习准备2. 向量减法的运算法则 （ 1 ）力的分解情境引入1F�2F�G�vsinvcosv情境引入（ 2 ）速度的分解MN2e�1e�探究：给定平面内任意两个向量 、 ,请你作出向量 ，平面内任一向量是否都可以在这两向量方向上分解呢？ �1e�2e21212,32eeeeDBAB分解平移共同起点1e2ea1e1e2eaa2eOABOBOAa11eOA22eOB2211eea思考：若 共线呢？21,ee帮助一 : 平面向量基本定理我们把不共线的向量 ， 叫做表示这一平面内所有向量的一组基底，记为：�1e�2e2e e1， 如果 , 是同一平面内的两个不共线的向量，那么对于这一平面内的任意向量 ，存在唯一一对实数、 ，使�1e�2ea122211eea 二：向量的夹角ab已知两个非零向量 和 。如图作 则 叫做向量 和 的夹角。,,bOBaOA)1800(00AOBab显然，当 时， 与 同向； 当 时， 与 反向。如果 与 的夹角是 ，我们说 与 垂直，记作 。00aaaabbbb090ba 0180baAOB 4 、定理的价值何在？ 2 、基底 、 是否可以选择？1e�2e�3 、定理中 、 的值是否唯一？1a2a思考1 、为什么基底 、 必须不共线？2e1e 例 1 、已知向量 ，求作向量21 ee、2135.2ee 三、例题讲解1e2e思考：你能想到几种作法？例例 2.2.已知： 已知： ABCDABCD 的两条对角线相交于点的两条对角线相交于点MM ，，MMBBAACCDD.MAMD�请同学们自选基底表示向量和试一试：例例 2.2.已知： 已知： ABCDABCD 的两条对角线相交于点的两条对角线相交于点MM ，，且 且 AB = a ,AD = b ,AB = a ,AD = b , 用 用 a ,b a ,b 表示表示MAMA 和 和 MDMDMMBBAACCDDbbaa.MAMDDB��为了求和， 关键是先求AC,分析：111()222MAACabab�111222MDDBab�课堂练习oABM12 ab（）a bMAOBABOAOB�已知点是三角形的边的中点，若＝ ，＝ ，则OM 知识总结：（ 1 ）平面向量基本定理 ;（ 2 ）向量的夹角。（ 3 ）平面向量基本定理的应用 ;（ 4 ）三角形中线的向量表示式 ;合作交流 自我总结思考思考实数运算？任意向量运算基底向量运算 作业：课本第 92 页 第 12题 莅临指导 !