正余弦函数的图象和性质VIP免费

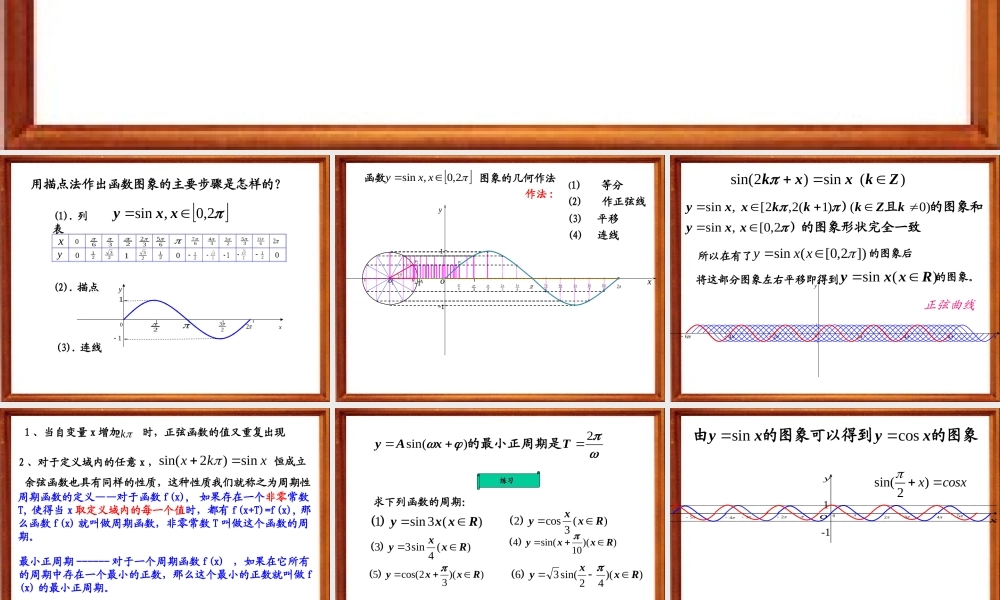
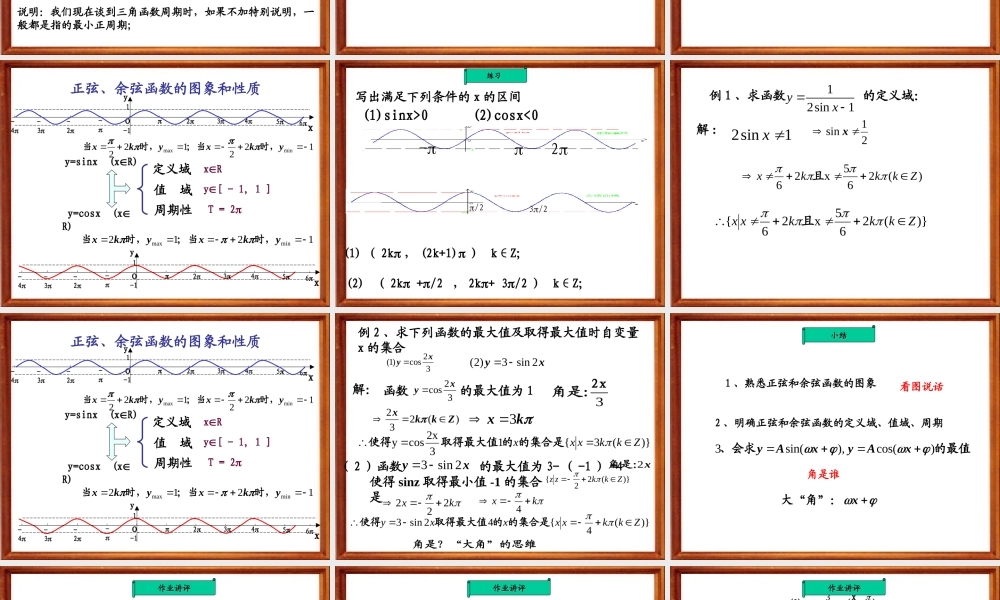
正弦、余弦函数的图象和性质（ 1 ）复习目标1 、熟悉正弦和余弦函数的图象2 、明确正弦和余弦函数的定义域、值域、周期的最值、会求)cos(),sin(3xAyxAy看图说话角是谁(1). 列表(2). 描点(3). 连线632326567342335611202123012123212300212312,0,sinxxy用描点法作出函数图象的主要步骤是怎样的？---223xy0211---xy 函数2,0,sinxxy图象的几何作法oxy---11---1--1oA作法 :(1) 等分3232656734233561126(2) 作正弦线(3) 平移61P1M/1p(4) 连线所以在有了])2,0[(sinxxy的图象后将这部分图象左右平移即得到)(sinRxxy的图象。2o46246xy---------1-1正弦曲线）的图象形状完全一致的图象和且）2,0[,sin)0()1(2,2[,sinxxykZkkkxxy)(sin)2sin(Zkxxk1 、当自变量 x 增加 时，正弦函数的值又重复出现sin(2)sinxkx2 、对于定义域内的任意 x ，恒成立2k周期函数的定义——对于函数 f(x), 如果存在一个非零常数T, 使得当 x 取定义域内的每一个值时，都有 f(x+T)=f(x), 那么函数 f(x) 就叫做周期函数，非零常数 T 叫做这个函数的周期。余弦函数也具有同样的性质，这种性质我们就称之为周期性最小正周期 ------ 对于一个周期函数 f(x) ，如果在它所有的周期中存在一个最小的正数，那么这个最小的正数就叫做 f(x) 的最小正周期。说明：我们现在谈到三角函数周期时，如果不加特别说明，一般都是指的最小正周期；求下列函数的周期：)(3sin1Rxxy）（)(3cos2Rxxy）（)(4sin33Rxxy）（))(10sin(4Rxxy）（))(32cos(5Rxxy）（))(42sin(36Rxxy）（练习练习2)sin(TxAy的最小正周期是xyo1-1023452345sin()2xcosx 的图象的图象可以得到由xyxycossin 正弦、余弦函数的图象和性质 x6yo--12345-2-3-41y=sinx (xR) x6o--12345-2-3-41y y=cosx (xR) 定义域值 域周期性xRy[ - 1, 1 ]T = 2122122minmaxykxykx时，；当时，当1212minmaxykxykx时，；当时，当写出满足下列条件的 x 的区间(1)sinx>0 (2)cosx<02-/23/2(1) （ 2k ， (2k+1)...