直线与椭圆的位置关系VIP免费

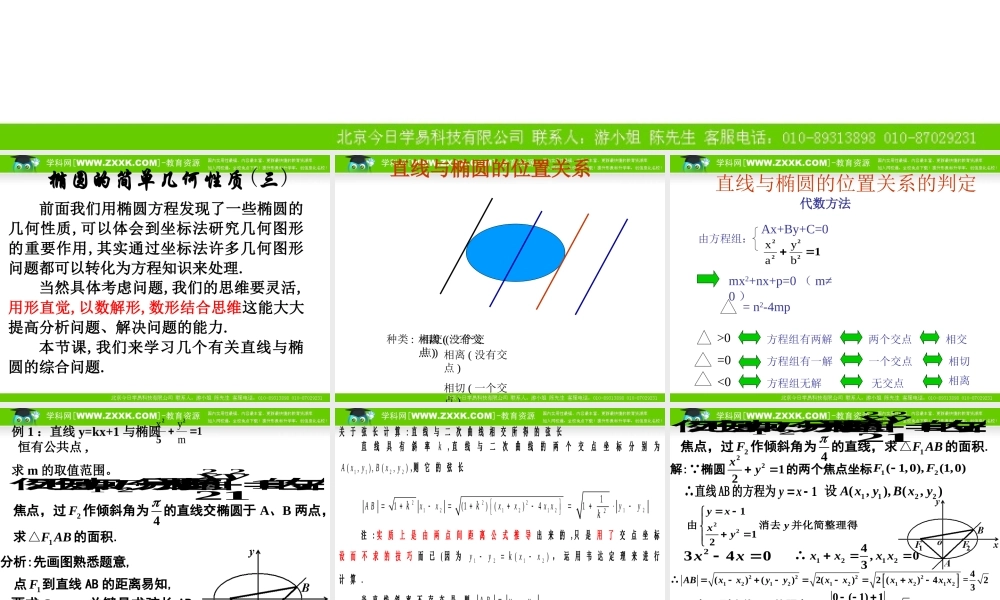
直线与椭圆的位置关系直线与椭圆的位置关系椭圆的简单几何性质(三) 前面我们用椭圆方程发现了一些椭圆的几何性质,可以体会到坐标法研究几何图形的重要作用,其实通过坐标法许多几何图形问题都可以转化为方程知识来处理. 当然具体考虑问题,我们的思维要灵活,用形直觉,以数解形,数形结合思维这能大大提高分析问题、解决问题的能力. 本节课,我们来学习几个有关直线与椭圆的综合问题. 椭圆的简单几何性质(三) 直线与椭圆的位置关系种类 : 相离 ( 没有交点 )相切 ( 一个交点 )相交 ( 二个交点 ) 相离 ( 没有交点 )相切 ( 一个交点 )相交 ( 二个交点 ) 直线与椭圆的位置关系的判定mx2+nx+p=0 （ m≠ 0 ）Ax+By+C=0由方程组：<0方程组无解相离无交点=0方程组有一解相切一个交点>0相交方程组有两解两个交点代数方法= n2-4mp12222 byax例 1 ：直线 y=kx+1 与椭圆 恒有公共点 ,求 m 的取值范围。1522 myx例2:已知点1 2FF、分别是椭圆2 2121xy的左、右 焦点，过2F 作倾斜角为 4 的直线交椭圆于 A、B 两点，求1F AB△的面积. 分析:先画图熟悉题意, 点1F 到直线 AB 的距离易知, 要求1F ABS△,关键是求弦长 AB. 设1122(,),(,)A xyB xy. 由直线方程和椭圆方程联立方程组 关 于 弦 长 计 算 : 直 线 与 二 次 曲 线 相 交 所 得 的 弦 长 直线具有斜率k, 直线与二次曲线的两个交点坐标分别为1122(,) ,(,)AxyBxy, 则 它 的 弦 长 2221212121(1)()4A Bxxxxx xkk1211yy2k 注: 实质上 是由两 点间 距离公 式推导 出来 的, 只是用 了交点 坐标设 而 不 求 的 技 巧 而 已 ( 因 为1212()yyxxk， 运 用 韦 达 定 理 来 进 行计 算 . 当 直 线 斜 率 不 存 在 是 , 则12A Byy. 焦点，过2F 作倾斜角为 4 的直线，求1F AB△的面积. 解: 椭圆2212xy 的两个焦点坐标 12( 1,0),(1,0)FF ∴直线 AB 的方程为1yx  由22112yxxy消去 y 并化简整理得 设1122(,),(,)A xyB xy 2340xx ∴12124 ,03xxx x ∴22221212121212()()2()2 ()4ABxxyyxxxxx x = 423 点1F 到直线 AB 的距离d  0( 1)12 =2 ∴112F ABSdAB  = 142223= 43 . 答: 1F AB△的...