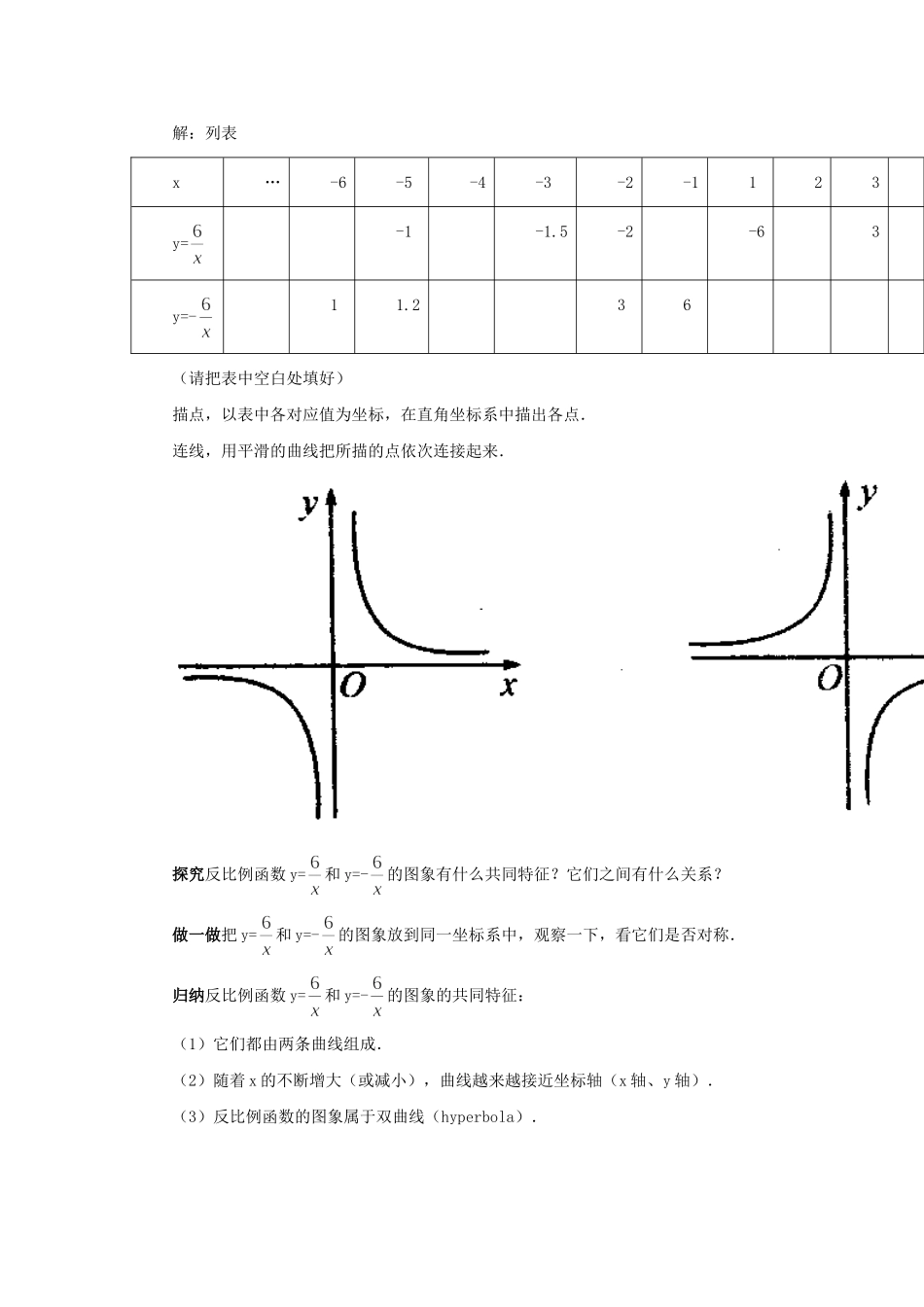
反比例函数的图象和性质教案教学目标1.知识与技能会画反比例函数的图象,并知道该图象与正比例函数、一次函数图象的区别,能从反比例函数的图象上分析出简单的性质.能用反比例函数的定义和性质解决实际问题.2.过程与方法通过画图象,进一步培养“描点法”画图的能力和方法,并提高对函数图象的分析能力同时尝试用类比和特殊到一般的思路方法,归纳反比例函数一些性质特征.3.情感、态度与价值观由图象的画法和分析,体验数学活动中的探索性和创造性,感受数学美,并通过图象的直观教学激发学习兴趣.教学重点难点重点:反比例函数图象的画法及探究,反比例函数的性质的运用.难点:反比例函数图象是平滑双曲线的理解及对图象特征的分析.课时安排 2 课时第 1 课时(一)创设情境,导入新课问题:1.若 y=是反比例函数,则 n 必须满足条件 n≠或 n≠-1.2.用描点法画图象的步骤简单地说是列表、描点、连线.3.试用描点法画出下列函数的图象:(1)y=2x;(2)y=1-2x.(二)合作交流,解读探究问题:我们已知道,一次函数 y=kx+b(k≠0)的图象是一条直线,那么反比例函数 y=(k 为常数且 k≠0)的图象是什么样呢?尝试用描点法来画出反比例函数的图象.画出反比例函数 y=和 y=-的图象.解:列表x…-6-5-4-3-2-1123y=-1-1.5-2-63y=-11.236(请把表中空白处填好)描点,以表中各对应值为坐标,在直角坐标系中描出各点.连线,用平滑的曲线把所描的点依次连接起来.探究反比例函数 y=和 y=-的图象有什么共同特征?它们之间有什么关系?做一做把 y=和 y=-的图象放到同一坐标系中,观察一下,看它们是否对称.归纳反比例函数 y=和 y=-的图象的共同特征:(1)它们都由两条曲线组成.(2)随着 x 的不断增大(或减小),曲线越来越接近坐标轴(x 轴、y 轴).(3)反比例函数的图象属于双曲线(hyperbola).此外,y=的图象和 y=-的图象关于 x 轴对称,也关于 y 轴对称.做一做在平面直角坐标系中画出反比例函数 y=和 y=-的图象.交流两个函数图象都用描点法画出?【分析】由 y=和 y=-的图象及 y=和 y=-的图象知道,(1)它们有什么共同特征和不同点?(2)每个函数的图象分别位于哪几个象限?(3)在每一个象限内,y 随 x 的变化而如何变化?猜想反比例函数 y=(k≠0)的图象在哪些象限由什么因素决定?在每一个象限内,y随 x 的变化情况如何?它可能与坐标轴相交吗?【归纳】(1)反比例函数 y=(k...