高中数学 基本不等式11课件 新人教A版必修5 课件VIP免费

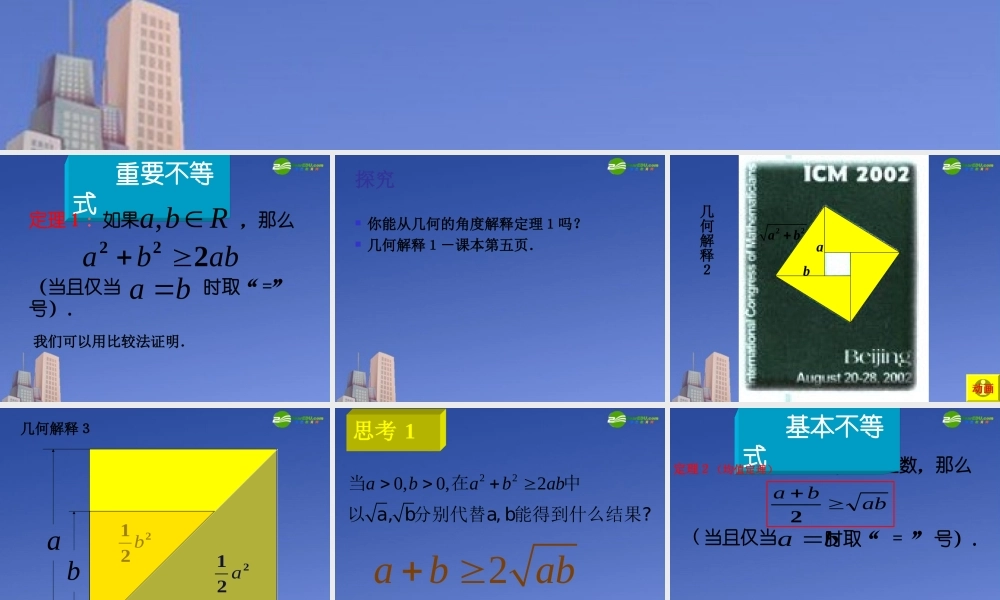
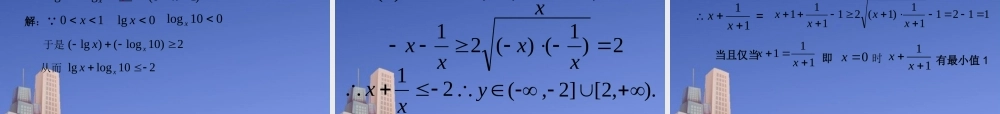2abab 重要不等式定理１：如果 ，那么 （当且仅当 时取“ =”号）．Rba,abba222ba 我们可以用比较法证明．探究 你能从几何的角度解释定理１吗？ 几何解释１－课本第五页．ab22ab动画几何解释２221 aab221 ba几何解释３ 思考 1220,0,2ababab当在中以 a, b分别代替a, b能得到什么结果?2abababba2( 当且仅当 时取“ = ” 号）． ba  如果 是正数，那么 ,a b 基本不等式定理２（均值定理）概念 如果ａ、ｂ都是正数，我们就称 为ａ、ｂ 的算术平均数， 称为ａ、ｂ的几何平均数。2abab均值定理可以描述为： 两个正数的算术平均数不小于（即大于或等于）它们的几何平均数ab.均值定理的几何意义2abab2ab半径不小于半弦DBCEoA2ababOCCDaD 当且仅当 中的“ = ” 号成立． ba 时2abab这句话的含义是 : 思考 2ba abba2当ba abba2当 和成立的条件相同吗？ 如： 成立，而 不成立。abba222abba2)5()1(2)5()1(22)5()1(2)5()1( 思考 3abba222成立的条件 _______abba2成立的条件 ______a，b RabR，222abcabbcac（1） 典例探讨222abbcca222变式:求证: 2a +2b +2c例 1 求证：（２）已知, , ,a b c d都是正数，求证()()4abcd acbdabcd证明：由 , , ,a b c d 都是正数，得02abcdab cd02acbdac bd()()4abcd acbdabcd()()4abcd acbdabcd即2., ,a b c巳知均为正数, 求证:(a+b)(b+c)(c+a)8abc1.0,0,11: ()()4.ababab巳知求证 练习1例 2 求证：（ 1 ）在所有周长相同的矩形中，正方形的面积最大；（ 2 ）在所有面积相同的矩形中，正方形的周长最短。变形 .1 如果积 已知yx,都是正数，求证：xy 是定值 ,P 那么当 yx  时 , 和 yx 有最小值 2 P2 如果和 yx 是定值 ,S 那么当 yx  时 , 积 xy有最大值 214 S证：  Ryx, ∴ xyyx21 当 xyP （定值）时，2xyP 上式当 yx  时取“ =” ∴ 当 yx  时， xy有最小值2 P2 当 xyS ( 定值 ) 时， 2Sxy ∴ 214xyS 上式当 yx  时取“ =” ∴ 当 yx 时， 214xyS有最大值yx 2 P∴注意：1 、最值的含义（“≥...