高中数学 241函数的零点课件 新人教A版必修1 课件VIP免费

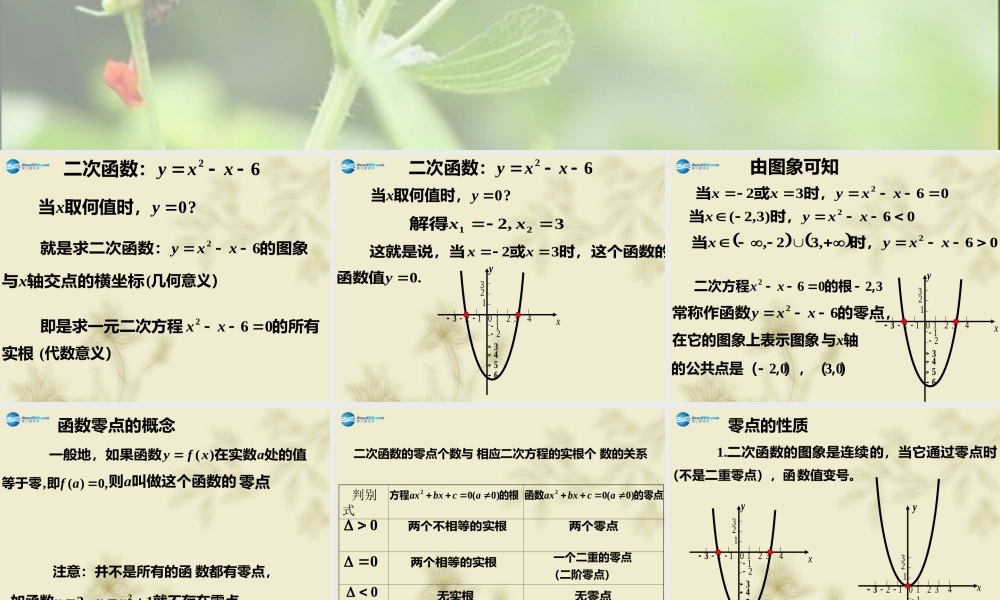
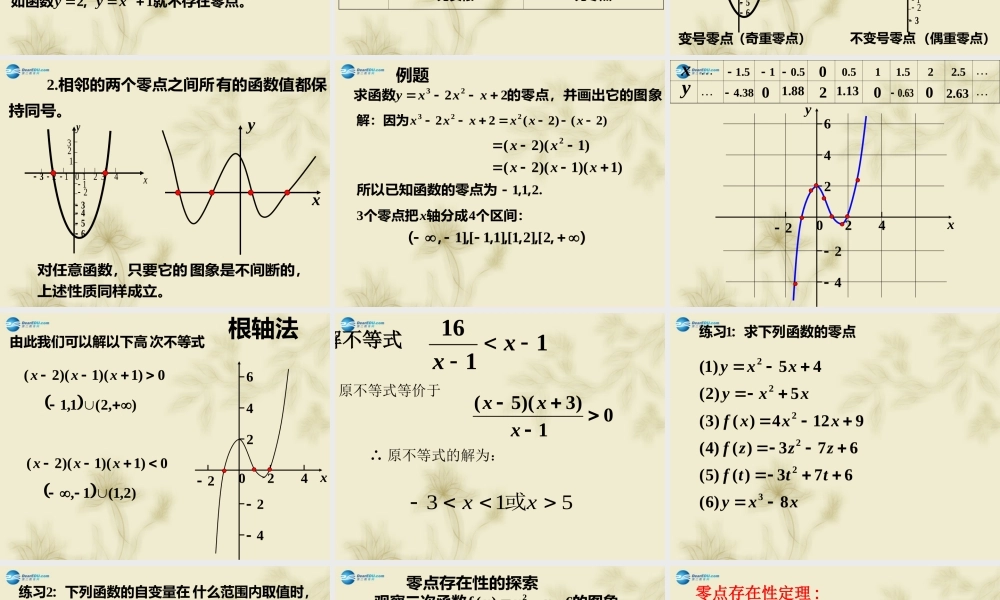
62xxy二次函数：?0yx取何值时，当的图象就是求二次函数：62xxy轴交点的横坐标与x的所有即是求一元二次方程062 xx实根几何意义）(代数意义）(62xxy二次函数：?0yx取何值时，当3,221xx解得时，这个函数的或这就是说，当32xx.0y函数值112 343102x2y3123456112 343102x2y3123456由图象可知06322xxyxx时，或当06)3,2(2xxyx时，当 06,32,2xxyx时，当32062，的根二次方程 xx的零点，常称作函数62xxy轴与在它的图象上表示图象x），），（，的公共点是（0302处的值在实数一般地，如果函数axfy)(,0)(,af即等于零叫做这个函数的则a零点数都有零点，注意：并不是所有的函就不存在零点。，如函数122 xyy函数零点的概念 判别式000的根方程)0(02acbxax的零点函数)0(02acbxax两个不相等的实根两个相等的实根无实根两个零点（二阶零点）一个二重的零点无零点数的关系相应二次方程的实根个二次函数的零点个数与零点的性质的，当它通过零点时二次函数的图象是连续.1数值变号。（不是二重零点），函112 343102x2y312345612 34102x3132y123变号零点不变号零点（奇重零点）（偶重零点）112 343102x2y3123456有的函数值相邻的两个零点之间所.2持同号。都保xy上述性质同样成立。图象是不间断的，对任意函数，只要它的象的零点，并画出它的图求函数2223xxxy)2()2(22223xxxxxx解：因为)1)(1)(2()1)(2(2xxxxx.211 ，，所以已知函数的零点为 个区间：轴分成个零点把43x），，，，，，，（2[]21[]11[]1例题… ………xy5.15.05.01015.125.238.4088.1213.1063.0063.2xy242244260x2422442600)1)(1)(2(xxx次不等式由此我们可以解以下高0)1)(1)(2(xxx),2(1,1)2,1(1,根轴法解不等式1116xx01)3)(5(xxx513xx或原不等式等价于∴ 原不等式的解为：：求下列函数的零点练习1xxytttfzzzfxxxfxxyxxy8)6(673)()5(673)()4(9124)()3(5)2(45)1(322222：或等于，小于函数值大于什么范围内取值时，：下列函数的自变量在练习0002102)1(2xxy32...