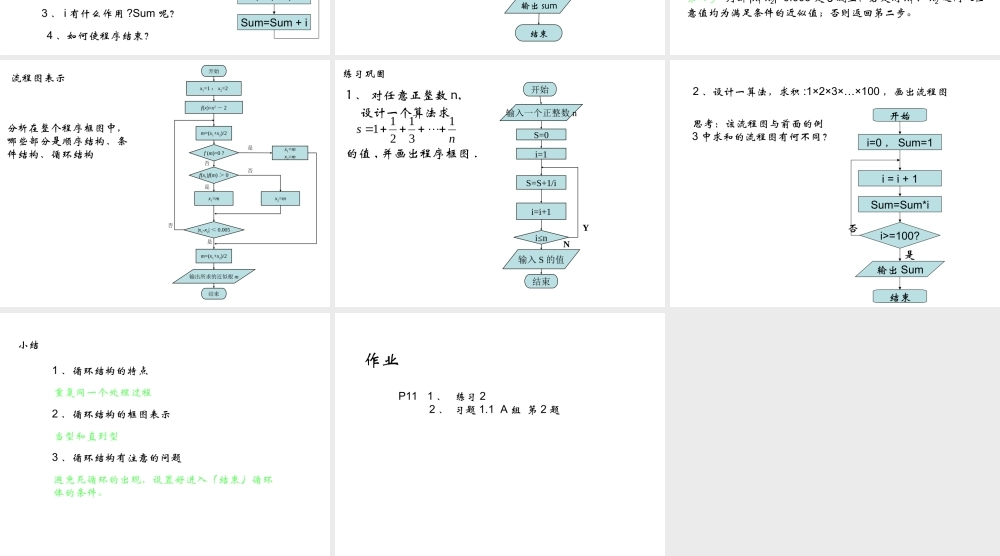
§1.1.2 程序框图算法初步 知识回忆1 、程序框图的概念2 、程序框图的图示和意义3 、顺序结构和条件结构的特点 程序框图又称流程图,是一种用规定的图形,指向线及文字说明来准确、直观地表示算法的图形。程序框名称功能终端框(起止框)表示一个算法的起始和结束输入、输出框表示算法的输入和输出的信息处理框(执行框)赋值、计算判断框判断一个条件是否成立,用“是”、“否”或“ Y” 、“ N” 标明 例 1 设计一算法,求和 :1+2+3+…+100第一步:确定首数 a ,尾数 b ,项数 n ;第二步:利用公式“总和 =( 首数 + 尾数) ×项数 /2” 求和;第三步:输出求和结果。算法 1 :开始结束输入 a,b,nSum=(a+b)*n/2输出 Sum 例 1 设计一算法,求和 :1+2+3+…+100算法 2 :第一步:从 1 开始将自然数 1 、 2 、 3 、…、 100 逐个相加 ;第二步:输出累加结果。思考: 1 、上边的式子有怎样的规律呢?Sum=0Sum=Sum + 1Sum=Sum + 2Sum=Sum + 3…Sum=Sum + 1002 、怎么用程序框图表示呢?i = i + 1Sum=Sum + i4 、如何使程序结束?3 、 i 有什么作用 ?Sum 呢?Sum=Sum + i 程序框图 如图开始i=1sum=0i=i+1sum=sum+1i≤100?输出 sum结束否是 例 2 用二分法求解方程求关于 x 的方程 x2 - 2 = 0 的根,精确到 0.005算法描述第一步 令 f(x)=x2-2 ,以为 f(1)<0 , f(2)>0 ,所以设 x1=1 , x2=2第二步 令 m=(x1+x2)/2 ,判断 f(m) 是否为 0 ,若是,则 m 为所求,否则,则继续判断 f(x1)·f(m) 大于 0 还是小于 0 。第三步 若 f(x1)·f(m) >0 则令 x1=m ,否则 x2=m 。第四步 判断 |x1-x2|<0.005 是否成立?若是则 x1 、 x2 之间人任意值均为满足条件的近似值;否则返回第二步。 开始x1=1 : x2=2f(x)=x2 - 2x1=mx2=mm=(x1+x2)/2x1=mx2=mf (m)=0 ?f(x1)f(m) > 0|x1-x2| < 0.005结束输出所求的近似根 mm=(x1+x2)/2是否否是否是流程图表示分析在整个程序框图中,哪些部分是顺序结构、条件结构、循环结构 1 、 对任意正整数 n,ns131211的值 , 并画出程序框图 .开始输入一个正整数 n输入 S 的值结束S=0i=1S=S+1/ii=i+1i≤nYN设计一个算法求练习巩固 2 、设计一算法,求积 :1×2×3×…×100 ,画出流程图结束输出 Sumi=0 , Sum=1开始i = i + 1Sum=Sum*ii>=100?否是思考:该流程图与前面的例3 中求和的流程图有何不同? 小结1 、循环结构的特点2 、循环结构的框图表示3 、循环结构有注意的问题避免死循环的出现,设置好进入(结束)循环体的条件。当型和直到型重复同一个处理过程 作业P11 1 、 练习 2 2 、 习题 1.1 A 组 第 2 题