1.3.1利用导数判断函数的单调性VIP免费

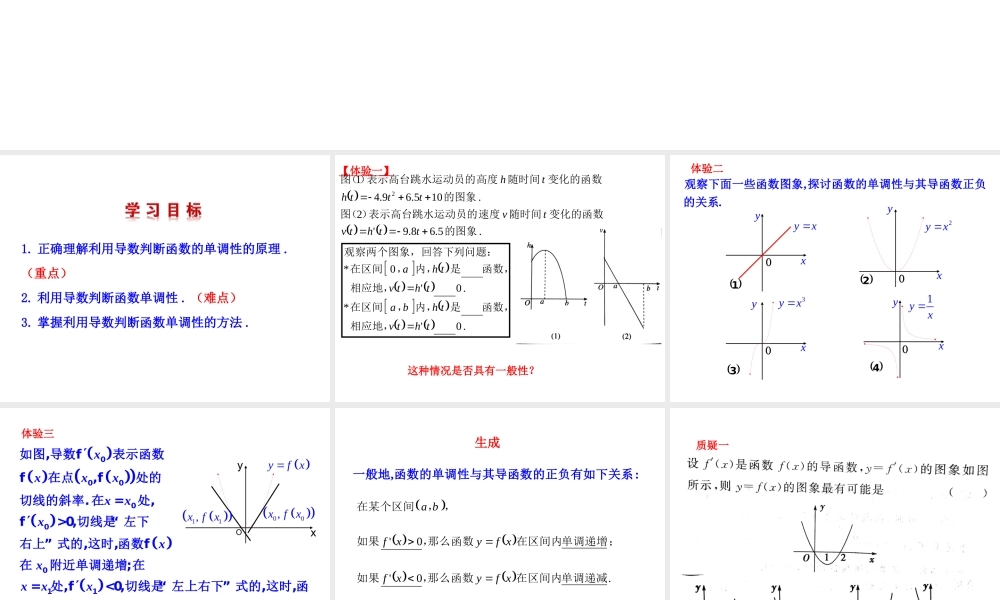
1.3 导数在研究函数中的应用 1.3.1 函数的单调性与导数 1. 正确理解利用导数判断函数的单调性的原理 . （重点） 2. 利用导数判断函数单调性 . （难点） 3. 掌握利用导数判断函数单调性的方法 .【体验一】   .5.68.9'2.105.69.412的图象变化的函数随时间速度表示高台跳水运动员的）（图的图象变化的函数随时间高度表示高台跳水运动员的）（图tthtvtvttthth      .0'*.0'0*thtvthbathtvtha相应地，函数，是，内，在区间相应地，函数，是，内，在区间列问题：观察两个图象，回答下这种情况是否具有一般性？,.观察下面一些函数图象 探讨函数的单调性与其导函数正负的关系yxyxO 12yxOyx 23yxOyx 31yxOyx 4OOOO体验二3.33图 yf xOyx 00,xf x 11,xf x   xxxxxxxxxxxxxx000000111如图,导数表示函数f在点,f处的切线的斜率.在 =处,>0,切线是“ 左下右上” 式的,这时,函数f在附近单调递增;在= 处,<0,切线是“ 左上右下” 式的,这时,函数f在 附近fff单调递减.体验三,:一般地 函数的单调性与其导函数的正负有如下关系生成    .0'0'单调递减在区间内那么函数，如果；单调递增在区间内那么函数，如果，，在某个区间xfyxfxfyxfba质疑一 求下列函数的单调区间： (1)y＝23x3－2x2＋3；(2)y＝ln(2x＋3)＋x2. 拓展二[思路探究] 求定义域 → 求导数 → 解不等式y′＜0和y′＞0 → 写单调区间 (1) 函数的定义域为 R.y′ ＝ 2x2 － 4x ＝ 2x(x － 2) ．令 y′ ＞ 0 ，则 2x(x － 2) ＞ 0 ，解得 x ＜ 0 或 x ＞ 2.所以函数的单调递增区间为 ( － ∞， 0) ， (2 ，＋∞ ) ．令 y′ ＜ 0 ，则 2x(x － 2) ＜ 0 ，解得 0 ＜ x ＜ 2.所以函数的单调递减区间为 (0,2) ．(2)函数 y＝ln(2x＋3)＋x2 的定义域为－32，＋∞ . y′＝22x＋3＋2x＝4x2＋6x＋22x＋3＝22x＋1x＋12x＋3. 令 y′＞0，解得－32＜x＜－1 或 x＞－12. 所以函数的单调递增区间为－32，－1 ，－12，＋∞ . 令 y′＜0，解得－1＜x＜－12， 所以函数的单调递减区间为－1，－12 . 利用导数求函数的单调区间的方法和步骤：(1) 求定义域；(2) 解不等式 f′(x)>0( 或 f′(x)<0) ；(3) 把不等式的解集与定义域求交集得单调区间．特别提醒： (1) 单调区间不能“并”，即不能用“∪”符号连接，只能用“，”或“和”隔开．(2) 导数法求得的单调区间一般用开区间表示．授人以渔