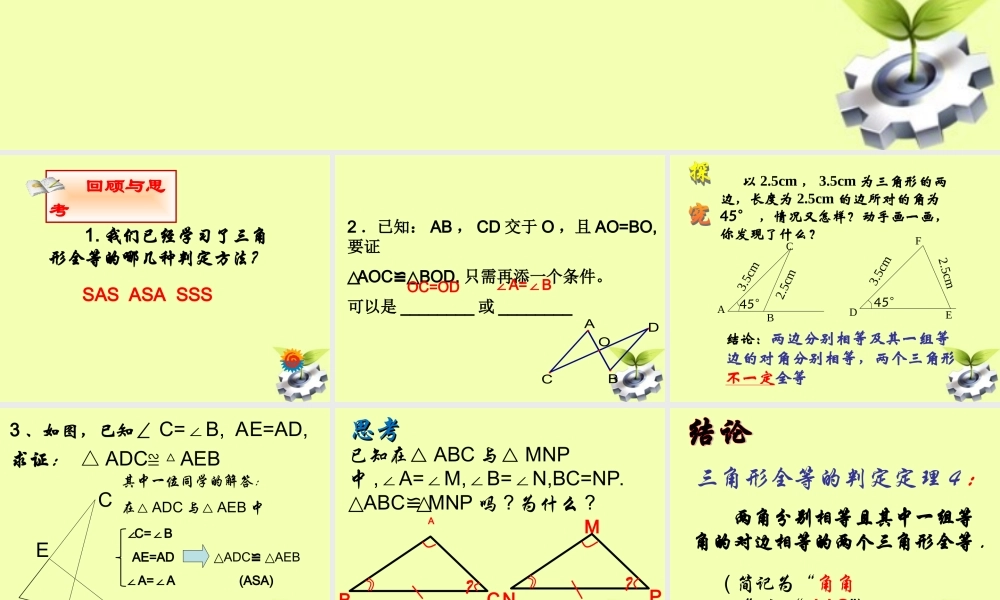
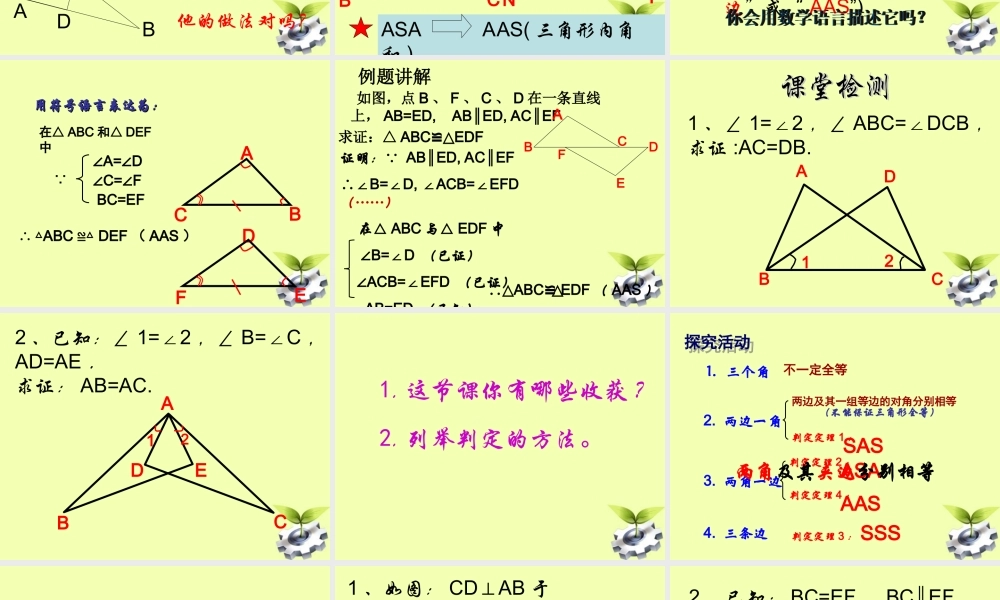
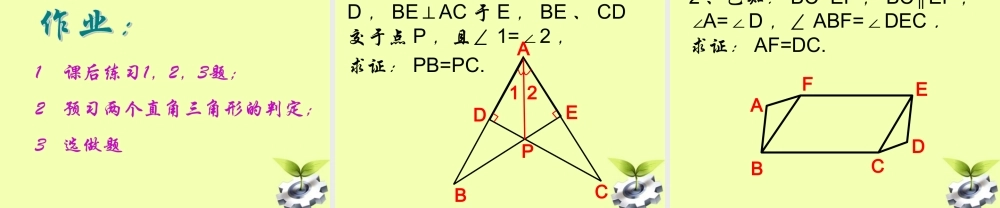
14.214.2 全等三角形的判定全等三角形的判定 (4)(4)AASAAS舒庄中心学校 张晓倩舒庄中心学校 张晓倩 1. 我们已经学习了三角形全等的哪几种判定方法?SAS ASA SSS 回顾与思考2 .已知: AB , CD 交于 O ,且 AO=BO,要证△AOCBOD,≌△只需再添一个条件。可以是 ________ 或 ________DBACOOC=OD∠A=B∠ 以 2.5cm , 3.5cm 为三角形的两边,长度为 2.5cm 的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm45°45°3.5cm2.5cm结论:两边分别相等及其一组等边的对角分别相等,两个三角形不一定全等3 、如图,已知∠ C=B, AE=AD,∠求证: △ ADC ≌ △ AEB CEBDA其中一位同学的解答:在△ ADC 与△ AEB 中 ∠C=B∠ AE=AD ADC△≌ AEB△ ∠A=A (ASA)∠他的做法对吗?已知在△ ABC 与△ MNP中 ,A=M,B=N,BC=NP.∠∠∠∠△ABCMNP≌△吗 ? 为什么 ?BCA?NPM?思考思考ASA AAS( 三角形内角和 ) 两角分别相等且其中一组等角的对边相等的两个三角形全等 .( 简记为“角角边”或“ AAS”)三角形全等的判定定理 4 :在△ ABC 和△ DEF中 ∴ △ABC DEF≌△( AAS )∠A= D∠∠C= F∠ BC=EF用符号语言表达为:用符号语言表达为:CBAFED∵例题讲解 如图,点 B 、 F 、 C 、 D 在一条直线上, AB=ED, AB ED, AC EF∥∥求证:△ ABCEDF≌△EDCFBA证明:∵ AB ED, AC EF∥∥∴∠B=D, ACB=EFD ∠∠∠(……) 在△ ABC 与△ EDF 中 ∠B=D ∠(已证) ∠ACB=EFD ∠(已证) AB=ED (已知)∴△ABCEDF≌△( AAS )1 、∠ 1=2∠ ,∠ ABC=DCB∠,求证 :AC=DB.BCAD122 、已知:∠ 1=2∠ ,∠ B=C∠,AD=AE .求证: AB=AC.ABCED121. 这节课你有哪些收获 ?2. 列举判定的方法。探究活动 探究活动 1. 三个角4. 三条边2. 两边一角3. 两角一边不一定全等SAS判定定理 1 :两边及其一组等边的对角分别相等判定定理 2 :ASA判定定理 4 :AAS(不能保证三角形全等)两角及其夹边分别相等判定定理 3 :SSS1 、如图: CDAB⊥于D , BEAC⊥于 E , BE 、 CD交于点 P ,且∠ 1=2∠ ,求证: PB=PC.DBPECA1 22 、已知: BC=EF , BC EF∥,∠A=D∠,∠ ABF=DEC∠.求证: AF=DC.ABFECD