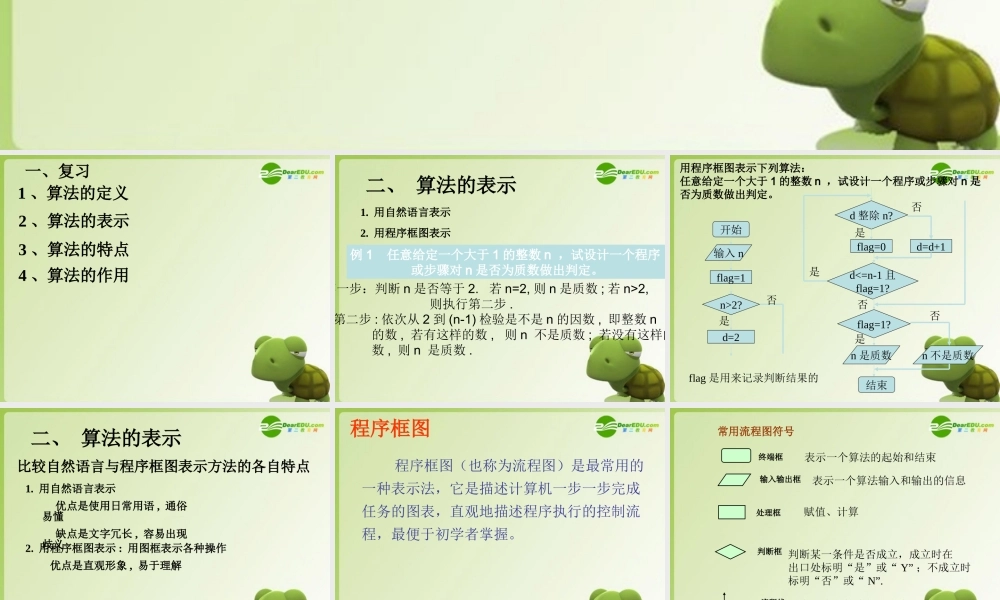
1.1.2 程序框图 一、复习1 、算法的定义2 、算法的表示3 、算法的特点4 、算法的作用 二、 算法的表示1. 用自然语言表示 2. 用程序框图表示第一步:判断 n 是否等于 2. 若 n=2, 则 n 是质数 ; 若 n>2, 则执行第二步 . 第二步 : 依次从 2 到 (n-1) 检验是不是 n 的因数 , 即整数 n 的数 , 若有这样的数 , 则 n 不是质数 ; 若没有这样的 数 , 则 n 是质数 . 例 1 任意给定一个大于 1 的整数 n ,试设计一个程序 或步骤对 n 是否为质数做出判定。 用程序框图表示下列算法:任意给定一个大于 1 的整数 n ,试设计一个程序或步骤对 n 是否为质数做出判定。开始输入 nflag=1n>2?d=2是d 整除 n?flag=0d<=n-1 且flag=1?flag=1?n 是质数结束是d=d+1否否n 不是质数否flag 是用来记录判断结果的是否是 二、 算法的表示1. 用自然语言表示 优点是使用日常用语 , 通俗易懂 缺点是文字冗长 , 容易出现歧义2. 用程序框图表示 : 用图框表示各种操作 优点是直观形象 , 易于理解 比较自然语言与程序框图表示方法的各自特点 程序框图程序框图(也称为流程图)是最常用的一种表示法,它是描述计算机一步一步完成任务的图表,直观地描述程序执行的控制流程,最便于初学者掌握。 终端框 处理框 输入输出框判断框流程线常用流程图符号表示一个算法的起始和结束表示一个算法输入和输出的信息判断某一条件是否成立,成立时在出口处标明“是”或“ Y” ;不成立时标明“否”或“ N”.赋值、计算表示流程的路径和方向 三种基本结构(表示一个良好算法的基本单元)① 顺序结构② 条件结构(选择结构)③ 循环结构ABPAB成立不成立 成立AP不成立AP成立不成立While (当型)循环 Until (直到型)循环 ① 顺序结构AB由若干个依次执行的处理步骤组成的。例 1 已知一个三角形的三边边长分别为 2 、 3 、 4 ,利用海伦 - 秦九韶公式设计一个算法,求出它的面积,画出它的程序框图 .()()()()3sp papbpcabcpabc 三角形面积为其中、 、 为三角形三边长开始输出 s结束2343p(2 )(3)(4 )spppp ② 条件结构(选择结构)PAB成立不成立算法的流程根据条件是否成立有不同的流向例 2 任意给定 3 个正实数,设计一个算法,判断分别以这 3 个数为三边边长的三角形是否存在 . 画出这个算法的程序框图 .开始输入 a 、 b ...