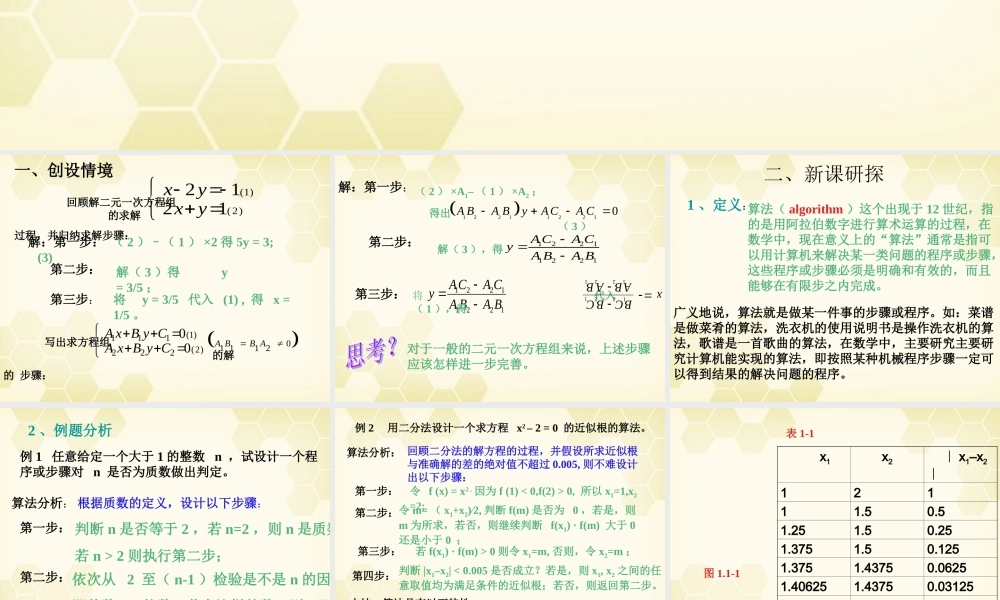
1.1.1 算法的概念 回顾解二元一次方程组 的求解过程,并归纳求解步骤: (1)(2)2121xyx y 解:第一步: ( 2 )–( 1 ) ×2 得 5y = 3; (3)第二步:解( 3 )得 y = 3/5 ;第三步:将 y = 3/5 代入 (1) , 得 x = 1/5 。 写出求方程组 的解的 步骤:(1)11101 11 2(2)22200A BB AA x B y CA x B y C一、创设情境 解:第一步: ( 2 ) ×A1– ( 1 ) ×A2 ; 得出 ( 3 )122112210A BA ByACA C第二步:解( 3 ),得12211221ACA CyA BA B第三步:12211221ACA CyA BA B将 代入( 1 ),得12211221BCB CxABA B对于一般的二元一次方程组来说,上述步骤应该怎样进一步完善。 二、新课研探1 、定义:广义地说,算法就是做某一件事的步骤或程序。如:菜谱是做菜肴的算法,洗衣机的使用说明书是操作洗衣机的算法,歌谱是一首歌曲的算法,在数学中,主要研究主要研究计算机能实现的算法,即按照某种机械程序步骤一定可以得到结果的解决问题的程序。算法( algorithm )这个出现于 12 世纪,指的是用阿拉伯数字进行算术运算的过程,在数学中,现在意义上的“算法”通常是指可以用计算机来解决某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成。 例 1 任意给定一个大于 1 的整数 n ,试设计一个程序或步骤对 n 是否为质数做出判定。算法分析: 根据质数的定义,设计以下步骤:第一步: 判断 n 是否等于 2 ,若 n=2 ,则 n 是质数;若 n > 2 则执行第二步;第二步:依次从 2 至( n-1 )检验是不是 n 的因数,即整数 n 的数,若有这样的数,则 n 不是质数;若没有这样的数,则 n 是质数。2 、例题分析 例 2 用二分法设计一个求方程 x2 – 2 = 0 的近似根的算法。算法分析: 回顾二分法的解方程的过程,并假设所求近似根与准确解的差的绝对值不超过 0.005, 则不难设计出以下步骤:第一步:令 f (x) = x2 , 因为 f (1) < 0,f(2) > 0, 所以 x1=1,x2=2;第二步:令 m= ( x1+x2)∕2, 判断 f(m) 是否为 0 ,若是,则m 为所求,若否,则继续判断 f(x1) · f(m) 大于 0 还是小于 0 ;第三步:若 f(x1) · f(m) > 0 则令 x1=m, 否则,令 x2=m ;第四步: 判断 |x1–x2|...