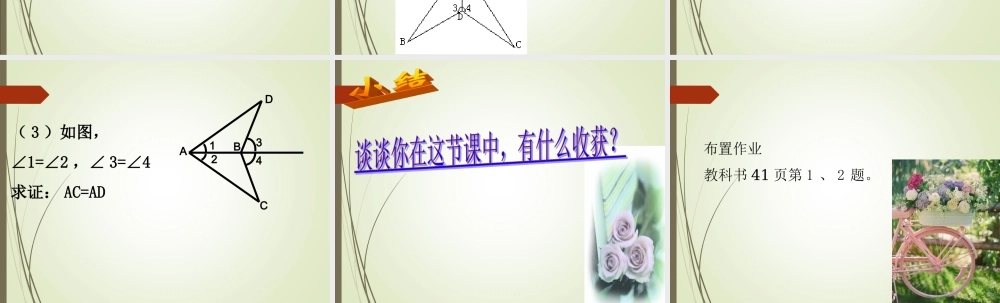
12.2 三角形全等的判定 ( 第 3 课时 ) 探究 4 先任意画出一个△ ABC ,再画一个△ A/B/C/ ,使 A/B/=AB , ∠A/ =A∠, ∠ B/ =B ∠(即两角和它们的夹边分别相等)。把画好的△ A/B/C/ ,放到△ ABC 上,它们全等吗?∠A=∠A/ (已知 ) AB=A/B/ (已知 )∠B=∠B/ (已知 )在△ ABC 和△ A/B/C/ 中 ∴ △ABC≌≌△ A/B/C/ ( ASA )用数学符号表示 : 两角和它们的夹边分别相等的两个三角形全等 ( 可以简写成“角边角”或“ ASA” )。探究反映的规律是:ACA’BC’B’如图 , 某同学把一块三角形的玻璃打碎成三片 , 现在他要到玻璃店去配一块形状完全一样的玻璃 , 那么最省事的办法是 ( )¢Û¢Ú¢Ù(A) 带①去 (B) 带②去 (C) 带③去 (D) 带①和②去C例 3 :已知,如图,点 D 在 AB 上,点 E 在 AC上, AB=AC ,∠ B=C∠,求证: AD=AE EDCBA( 1 )如图,∠ 1=∠2 ,∠ 3=∠4 ,若证得 BD=CD ,则所用的判定两三角形全等的依据是 ( )A. 角角角B .角边角 C .边角边 D .角角边练习:( 2 )在△ ABC 和△ DEF 中,已知 AB = DE ,∠ A=∠ D ,若补充下列条件中的任意一条,就能判定△ ABC≌≌△ DEF 的是 ( )①AC=DF ②BC=EF ③∠B=∠ E ④∠C=∠ FA .①②③ B .②③④ C .①③④ D .①②④( 3 )如图,∠1=∠2 ,∠ 3=∠4求证: AC=AD1234ADBC布置作业教科书 41 页第 1 、 2 题。