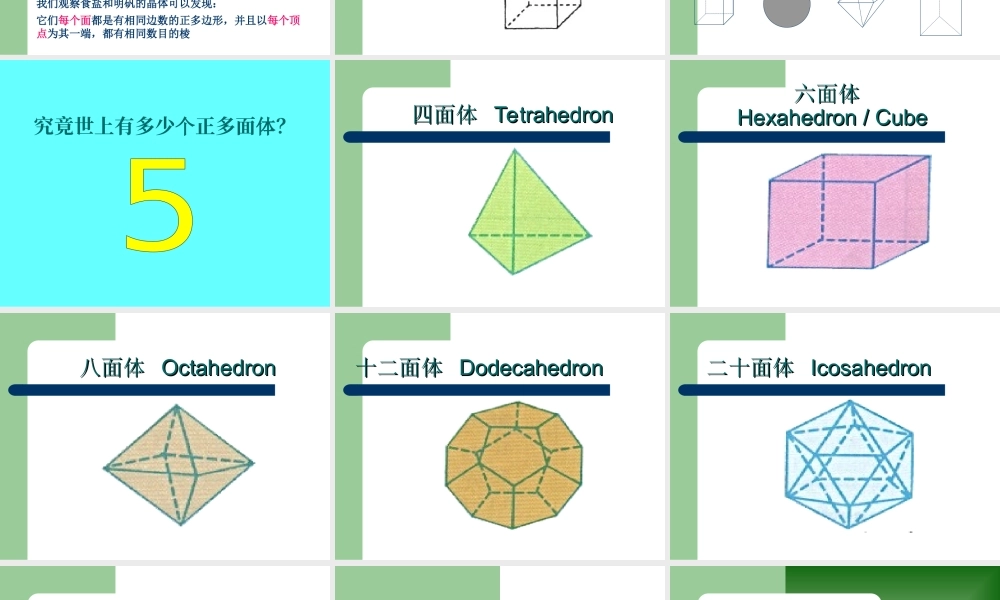
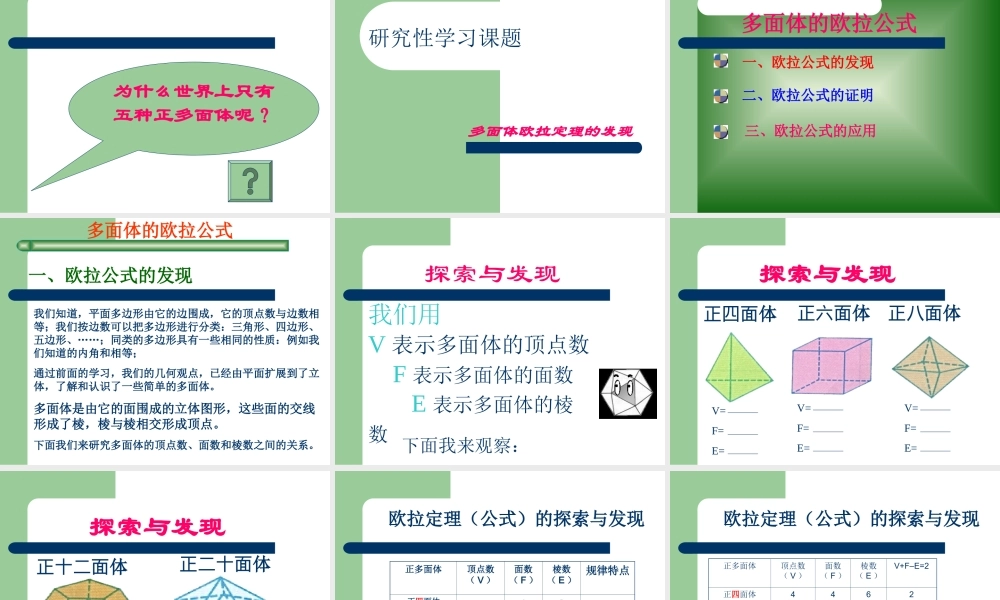
预备知识多面体和正多面体 多面体和正多面体介绍棱柱、棱锥都是一些平面多边形围成的几何体。若干个平面多边形围成的几何体,叫做多面体。围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,若干个面的公共顶点叫做多面体的顶点。许多矿物结晶体,都具有多面体的形状。例如:食盐晶体石膏晶体明矾晶体 多面体的分类第一种分类方法:把多面体的任何一个面伸展为平面,如果所有其他各面都在这个平面的同侧,这样的多面体叫做凸多面体(图 1 )图 1图 2想一想,图 2是凸多面体吗? 多面体的分类第二种分类方法:一个多面体至少有四个面。多面体依照它的面数分别叫做四面体、五面体、六面体等。例如,三棱锥是四面体,三棱柱是五面体,正方体是六面体等 正多面体食盐晶体明矾晶体我们观察食盐和明矾的晶体可以发现:它们每个面都是有相同边数的正多边形,并且以每个顶点为其一端,都有相同数目的棱 一般地,每个面都是有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体,叫做正多面体。正多面体例如:正方体就是一种正多面体 问题:以下哪些是多面体?哪些是正多面体呢?究竟世上有多少个正多面体? 四面四面体体 TetrahedronTetrahedron 六面六面体体 Hexahedron / CubeHexahedron / Cube 八面八面体体 OctahedronOctahedron 十二面十二面体体 DodecahedronDodecahedron 二十面二十面体体 IcosahedronIcosahedron 为什么世界上只有五种正多面体呢? 研究性学习课题多面体欧拉定理的发现 多面体的欧拉公式一、欧拉公式的发现二、欧拉公式的证明三、欧拉公式的应用 多面体的欧拉公式一、欧拉公式的发现我们知道,平面多边形由它的边围成,它的顶点数与边数相等;我们按边数可以把多边形进行分类:三角形、四边形、五边形、……;同类的多边形具有一些相同的性质:例如我们知道的内角和相等;通过前面的学习,我们的几何观点,已经由平面扩展到了立体,了解和认识了一些简单的多面体。多面体是由它的面围成的立体图形,这些面的交线形成了棱,棱与棱相交形成顶点。下面我们来研究多面体的顶点数、面数和棱数之间的关系。 我们用V 表示多面体的顶点数 F 表示多面体的面数 E 表示多面体的棱数 探索与发现下面我来观察: 正四面体正六面体正八面体V=F=E=V=F=E=V=F=E=探索与发现 正十二面体正二十面体探索与发现V=F=E=V=F=E= 正多面体顶点数( V )面数( F )棱数( ...