算法案例(第二课时) 人教版必修三第一章算法初步课件大全VIP免费

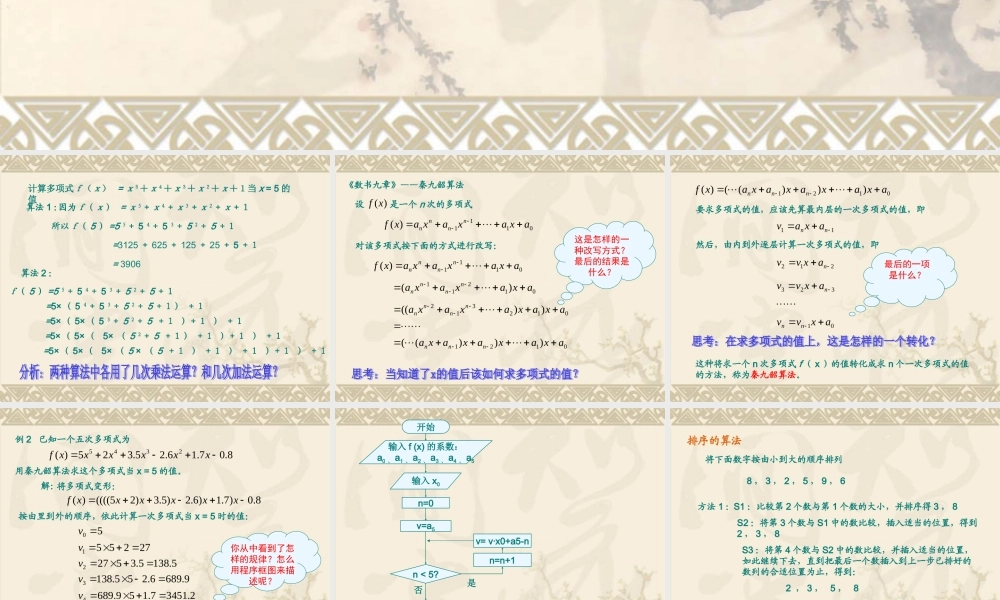
算法案例（第二课时） 计算多项式ｆ（ｘ） = ｘ５＋ｘ４＋ｘ３＋ｘ２＋ｘ＋１当 x = 5 的值算法 1 ：因为ｆ（ｘ） = ｘ５＋ｘ４＋ｘ３＋ｘ２＋ｘ＋１所以ｆ（ 5 ） =5 ５＋ 5 ４＋ 5 ３＋ 5 ２＋ 5 ＋１=3125 ＋ 625 ＋ 125 ＋ 25 ＋ 5 ＋１= 3906算法 2 ：ｆ（ 5 ） =5 ５＋ 5 ４＋ 5 ３＋ 5 ２＋ 5 ＋１=5× （ 5 ４＋ 5 ３＋ 5 ２＋ 5 ＋１） ＋１=5× （ 5× （ 5 ３＋ 5 ２＋ 5 ＋１ ）＋１ ） ＋１=5× （ 5× （ 5× （ 5 ２＋ 5 ＋１） ＋１ ）＋１ ） ＋１=5× （ 5× （ 5× （ 5 × （ 5 ＋１ ） ＋１ ） ＋１ ）＋１ ） ＋１ 《数书九章》——秦九韶算法0111)(axaxaxaxfnnnn设)(xf是一个 n 次的多项式对该多项式按下面的方式进行改写：0111)(axaxaxaxfnnnn01211)(axaxaxannnn012312))((axaxaxaxannnn0121)))((axaxaxaxannn这是怎样的一种改写方式？最后的结果是什么？ 0121)))(()(axaxaxaxaxfnnn要求多项式的值，应该先算最内层的一次多项式的值，即11nnaxav然后，由内到外逐层计算一次多项式的值，即212naxvv323naxvv01axvvnn最后的一项是什么？这种将求一个 n 次多项式 f （ x ）的值转化成求 n 个一次多项式的值的方法，称为秦九韶算法。 例 2 已知一个五次多项式为8.07.16.25.325)(2345xxxxxxf用秦九韶算法求这个多项式当 x = 5 的值。解：将多项式变形：8.0)7.1)6.2)5.3)25(((()(xxxxxxf按由里到外的顺序，依此计算一次多项式当 x = 5 时的值：272551v50 v5.1385.35272v9.6896.255.1383v2.34517.159.6894v2.172558.052.34515v所以，当 x = 5 时，多项式的值等于 17255.2你从中看到了怎样的规律？怎么用程序框图来描述呢？ 开始输入 f (x) 的系数：a0 、 a1 、 a2 、 a3 、 a4 、 a5输入 x0n=0v=a5v= v·x0+a5-nn=n+1n < 5?输出 v结束否是秦九韶算法检验注意：要想使用检验功能，请使用前，先要减低宏的安全限制 排序的算法将下面数字按由小到大的顺序排列8 ， 3 ， 2 ， 5 ， 9 ， 6方法 1 ：S1 ：比较第 2 个数与第 1 个数的...