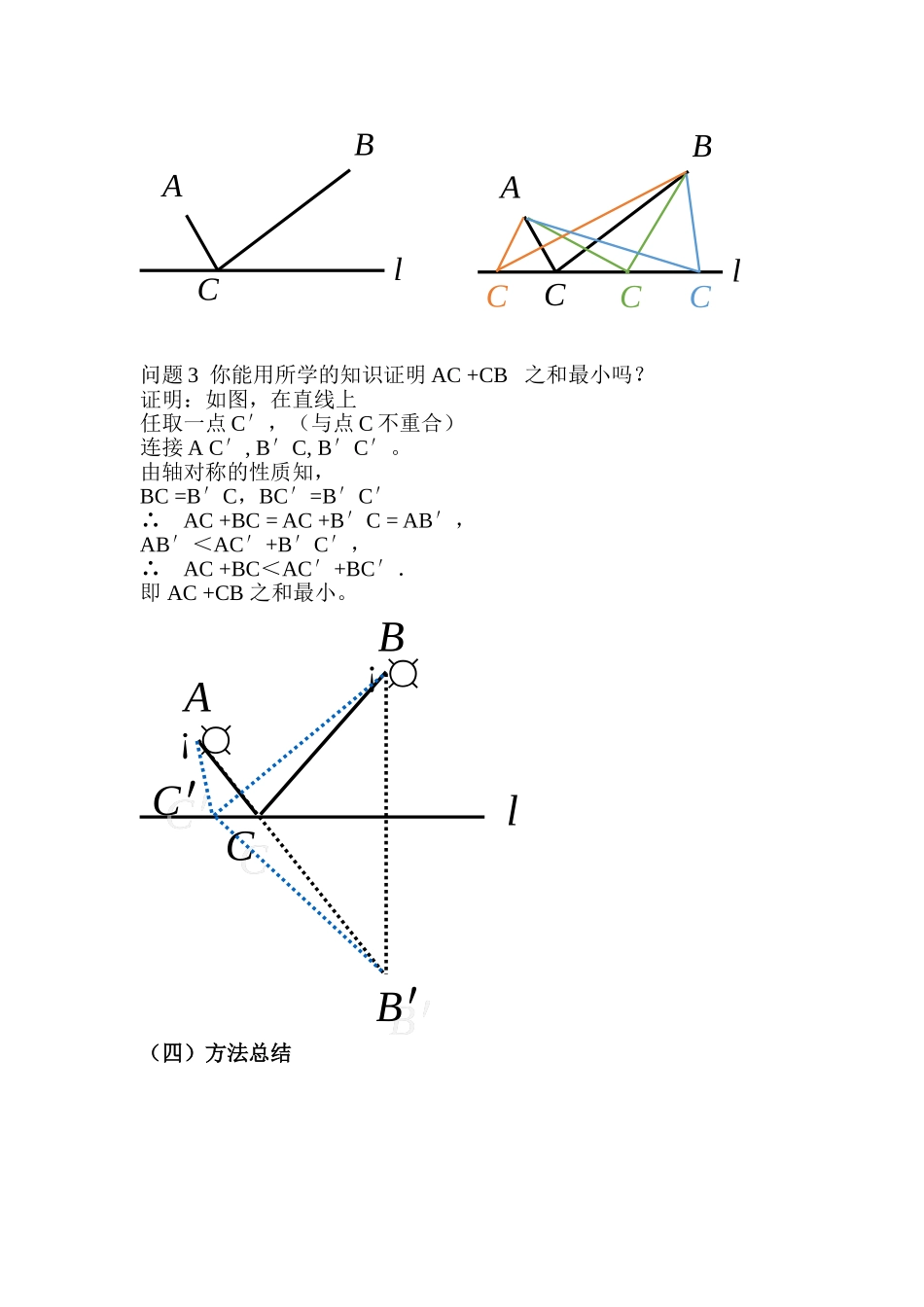
微课 《最短路径-将军饮马问题》教学设计博白县中学 张玉玲一、学习目标: 1.能利用轴对称解决简单的最短路径问题。2. 体会图形的变化在解决最值问题中的作用,感悟转化思想。二、重点:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题。难点:利用轴对称解决简单的最短路径问题。三、学前准备对“最短路径问题”的课题研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称将线段和最小问题转化为“两点之间,线段最短”(或“三角形两边之和大于第三边”)问题。四、教学过程(一)课前导入前面我们研究过一些关于“两点的所有连线中,线段最短”、“连接直线外一点与直线上各点的所有线段中,垂线段最短”等问题,我们称它们为最短路径问题,现实 生活中经常涉及到选择最短路径的问题,本课将利用所学知识 探究数学史中著名 的“将军饮马问题”。(2)引出问题问题 1 相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题: 将军从图中的 A 地出发,到一条笔直的河边 l 饮马,然后到营地B 处 .到河边什么地方饮马可使他所走的路线全程最短?(3)证明过程如图,点 A,B 在直线 l 的同侧,点 C 是直线上的一个动点,当点 C 在 l 的什么位置时,AC 与 CB 之和最小? BAll问题 3 你能用所学的知识证明 AC +CB 之和最小吗? 证明:如图,在直线上任取一点 C′,(与点 C 不重合)连接 A C′, B′C, B′C′。由轴对称的性质知, BC =B′C,BC′=B′C′∴ AC +BC = AC +B′C = AB′,AB′<AC′+B′C′,∴ AC +BC<AC′+BC′.即 AC +CB 之和最小。(四)方法总结BAlCBAlCCCCB¡¤lA¡¤B′B′CCC′C′B¡¤lA¡¤B′B′CCB¡¤lA¡A′A′CC