二次函数y=a(x—h)2的图象和性质VIP免费

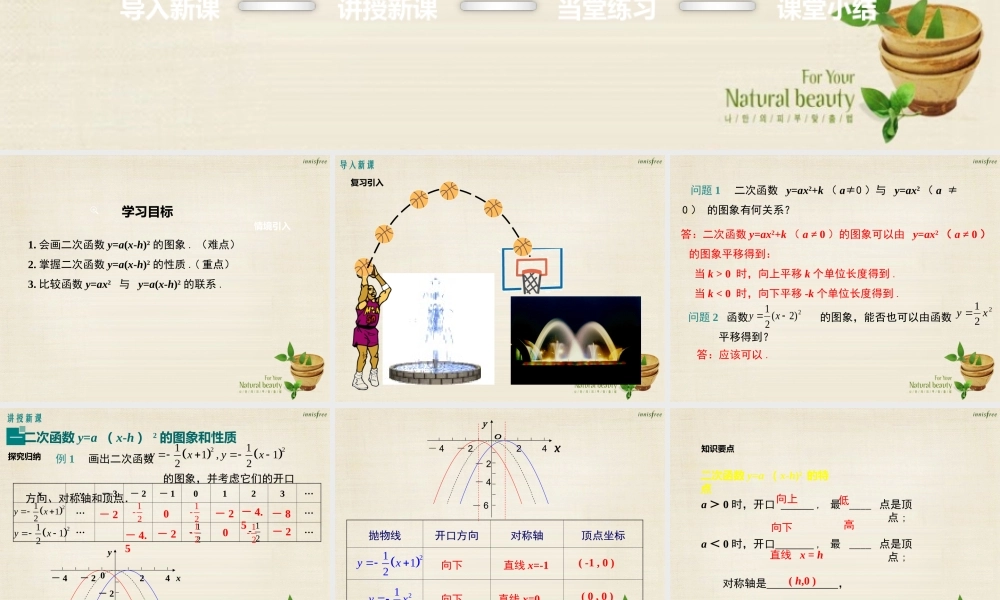
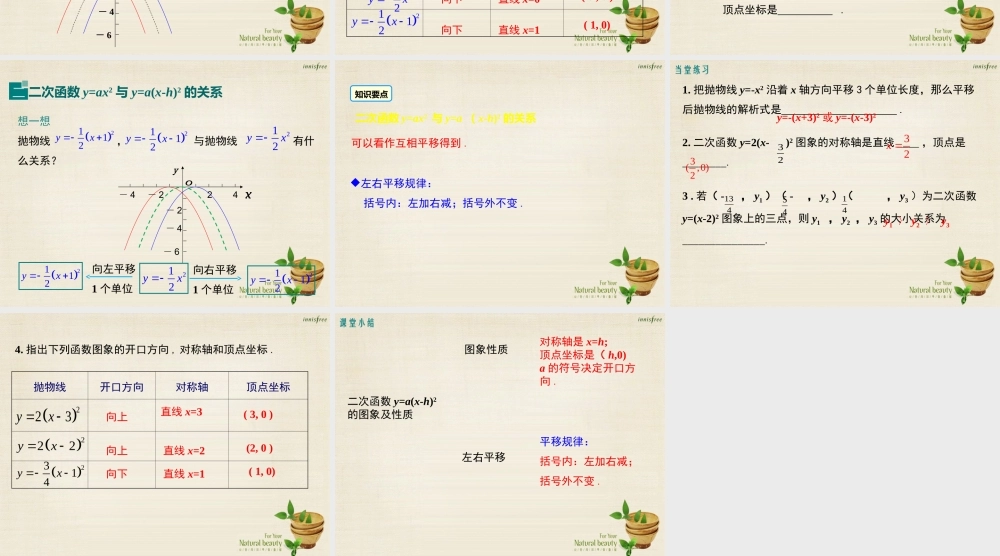
22.1.3 二次函数 y=a(x-h)2+k 的图象和性质第二十二章 二次函数导入新课讲授新课当堂练习课堂小结第 2 课时 二次函数 y=a （ x-h)2 的图象和性质情境引入学习目标1. 会画二次函数 y=a(x-h)2 的图象 . （难点）2. 掌握二次函数 y=a(x-h)2 的性质 .( 重点）3. 比较函数 y=ax2 与 y=a(x-h)2 的联系 .导入新课复习引入 问题 1 二次函数 y=ax2+k （ a≠0 ）与 y=ax2 （ a ≠ 0 ） 的图象有何关系？答：二次函数 y=ax2+k （ a ≠ 0 ）的图象可以由 y=ax2 （ a ≠ 0 ） 的图象平移得到： 当 k > 0 时，向上平移 k 个单位长度得到 . 当 k < 0 时，向下平移 -k 个单位长度得到 . 问题 2 函数 的图象，能否也可以由函数 平移得到？ 221 xy 2)2(21xy答：应该可以 .讲授新课二次函数 y=a （ x-h ） 2 的图象和性质一 例 1 画出二次函数 的图象，并考虑它们的开口方向、对称轴和顶点．22111,122yxyxx···－ 3－ 2－ 10123···············－ 2－ 4.5－ 200－ 2－ 21212－ 22－ 2－ 4－ 64－ 4探究归纳2112yx2112yx1- 21- 21- 21- 2－ 4.50xy－ 8－ 22－ 2－ 4－ 64－ 4抛物线开口方向对称轴顶点坐标向下直线 x=-1( -1 , 0 )直线 x=0直线 x=1向下向下( 0 , 0 )( 1, 0)2112yx2112yx212yxa ＞ 0 时，开口 , 最 ____ 点是顶点 ; a ＜ 0 时，开口 , 最 ____ 点是顶点 ; 对称轴是 ， 顶点坐标是 .向上低向下高直线 x = h( h,0 )知识要点二次函数 y=a （ x-h)2 的特点向右平移1 个单位二次函数 y=ax2 与 y=a(x-h)2 的关系二想一想 抛物线 ， 与抛物线 有什么关系？ 2112yx2112yx212yx－ 22－ 2－ 4－ 64－ 4212yx向左平移1 个单位2112yx2112yx知识要点二次函数 y=ax2 与 y=a （ x-h)2 的关系可以看作互相平移得到 .左右平移规律： 括号内：左加右减；括号外不变 .1. 把抛物线 y=-x2 沿着 x 轴方向平移 3 个单位长度，那么平移后抛物线的解析式是 .2. 二次函数 y=2(x- )2 图象的对称轴是直线 ____ ，顶点是________.3 . 若（ - ， y1 ）（ - ， y2 ）（ ， y3 ）为二次函数y=(x-2)2 图象上的三点，则 y1 ， y2 ， y3 的大小关系为_______________.当堂练习413454123 y=-(x+3)2 或 y=-(x-3)2 32x 3( ,0)2y1 〉 y2 〉 y3 4. 指出下列函数图象的开口方向 , 对称轴和顶点坐标 .抛物线开口方向对称轴顶点坐标向上直线 x=3( 3, 0 )直线 x=2直线 x=1向下向上(2, 0 )( 1, 0)2314yx223yx222yx课堂小结二次函数 y=a(x-h)2的图象及性质图象性质对称轴是 x=h;顶点坐标是（ h,0)a 的符号决定开口方向 .左右平移平移规律：括号内：左加右减；括号外不变 .