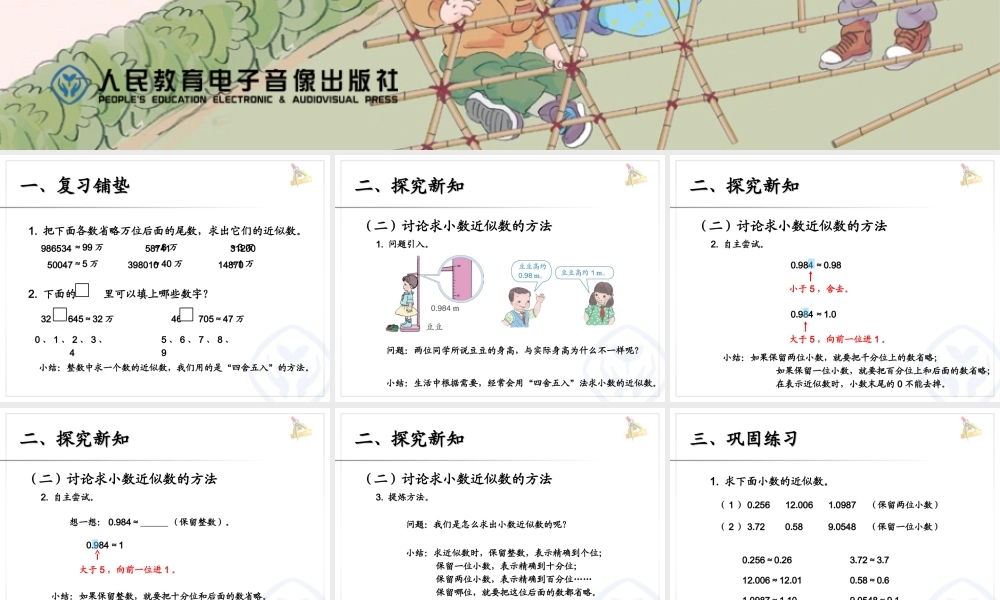
小数的近似数(例 1 ) 小数的意义和性质一、复习铺垫一、复习铺垫1. 把下面各数省略万位后面的尾数,求出它们的近似数。 986534 58741 31200 50047 398010 14870≈5 万≈6 万≈3 万≈99 万≈40 万≈1 万0 、 1 、 2 、 3 、45 、 6 、 7 、 8 、9小结:整数中求一个数的近似数,我们用的是“四舍五入”的方法。2. 下面的 里可以填上哪些数字? 32 645≈32 万 46 705≈47 万问题:两位同学所说豆豆的身高,与实际身高为什么不一样呢?小结:生活中根据需要,经常会用“四舍五入”法求小数的近似数。1. 问题引入。(二)讨论求小数近似数的方法二、探究新知二、探究新知0.984 小于 5 ,舍去。0.984 大于 5 ,向前一位进 1 。小结:如果保留两位小数,就要把千分位上的数省略; 如果保留一位小数,就要把百分位上和后面的数省略; 在表示近似数时,小数末尾的 0 不能去掉。≈0.98≈1.02. 自主尝试。二、探究新知二、探究新知(二)讨论求小数近似数的方法0.984 大于 5 ,向前一位进 1 。想一想: 0.984≈ (保留整数)。讨论:保留整数得到的“ 1” 和保留一位小数得到的“ 1.0” 一样吗?末尾的 0 能去掉吗?≈1小结:如果保留整数,就要把十分位和后面的数省略。二、探究新知二、探究新知2. 自主尝试。(二)讨论求小数近似数的方法问题:我们是怎么求出小数近似数的呢?小结:求近似数时,保留整数,表示精确到个位; 保留一位小数,表示精确到十分位; 保留两位小数,表示精确到百分位…… 保留哪位,就要把这位后面的数都省略。3. 提炼方法。二、探究新知二、探究新知(二)讨论求小数近似数的方法三、巩固练习三、巩固练习( 1 ) 0.256 12.006 1.0987 (保留两位小数)0.256≈0.2612.006≈12.011.0987≈1.10( 2 ) 3.72 0.58 9.0548 (保留一位小数)3.72≈3.70.58≈0.69.0548≈9.1监控:你是怎样取近似值的?1. 求下面小数的近似数。( 1 ) 4.46 0.339 4.05 (精确到十分位)( 2 ) 7.354 6.268 0.402 (省略百分位后面的尾数)4.46≈4.50.339≈0.34.05≈4.17.354≈7.356.268≈6.270.409≈0.40监控:你是怎样取近似值的?2. 求下面各小数的近似数。三、巩固练习三、巩固练习3. 按照要求写出表中小数的近似数。10.09.960.90.9151.551.462.02.00监控:说一说你是怎么想的。151210保留整数保留一位小数保留两位小数9.9560.90551.4631.995三、巩固练习三、巩固练习四、布置作业四、布置作业作业:作业:第 54 页练习十三,第 2 题。