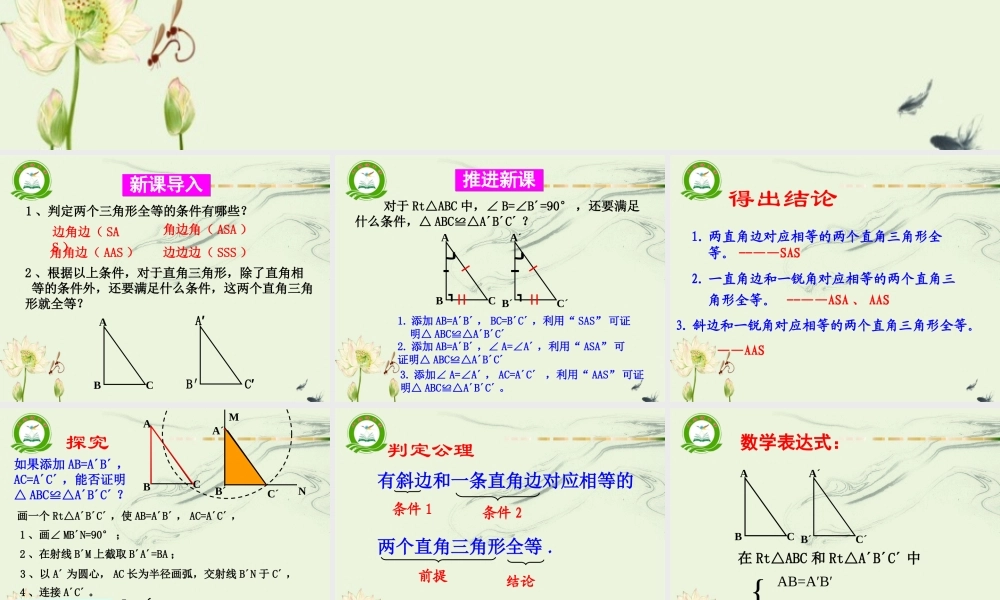
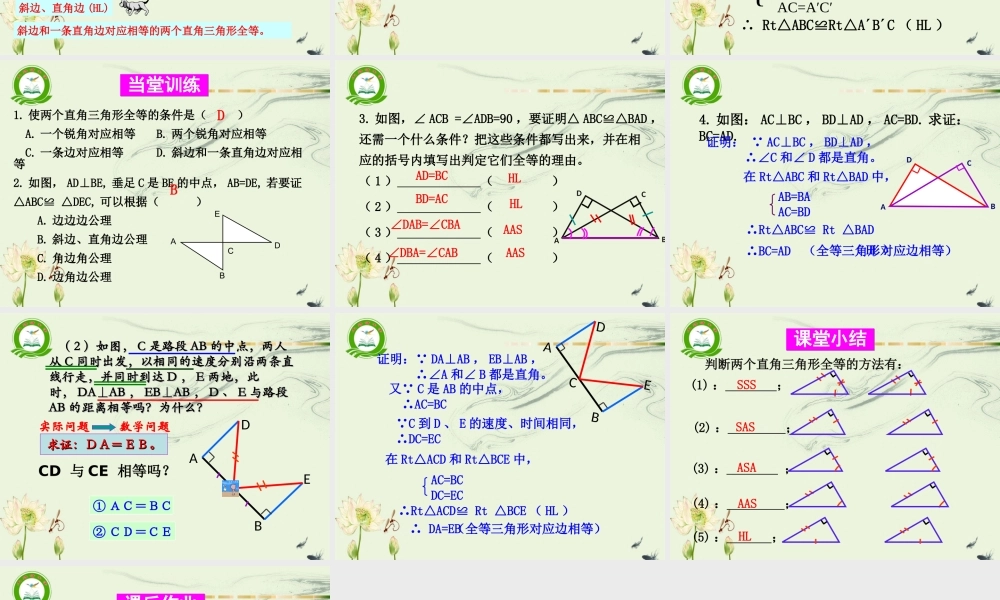
第 2 章 2.5 全等三角形直角三角形全等的判定湘教版八年级数学下册大路铺中学吴上民1 、判定两个三角形全等的条件有哪些?边角边( SAS )2 、根据以上条件,对于直角三角形,除了直角相 等的条件外,还要满足什么条件,这两个直角三角形就全等?ABCA′B′C′边边边( SSS )角角边( AAS )角边角( ASA )新课导入新课导入 对于 Rt△ABC 中,∠ B=∠B´=90° ,还要满足什么条件,△ ABC≌△A´B´C´ ?ABCA´B´C´1. 添加 AB=A´B´ , BC=B´C´ ,利用“ SAS” 可证明△ ABC≌△A´B´C´2. 添加 AB=A´B´ ,∠ A=∠A´ ,利用“ ASA” 可证明△ ABC≌△A´B´C´3. 添加∠ A=∠A´ , AC=A´C´ ,利用“ AAS” 可证明△ ABC≌△A´B´C´ 。┓┓推进新课推进新课得出结论1. 两直角边对应相等的两个直角三角形全等。 --——SAS2. 一直角边和一锐角对应相等的两个直角三角形全等。 --——ASA 、 AAS3. 斜边和一锐角对应相等的两个直角三角形全等。 ——AAS如果添加 AB=A´B´ ,AC=A´C´ ,能否证明 △ ABC≌△A´B´C´ ?ABCA´B´C´探究MN●●画一个 Rt△A´B´C´ ,使 AB=A´B´ , AC=A´C´ ,1 、画∠ MB´N=90° ;2 、在射线 B´M 上截取 B´A´=BA ;3 、以 A´ 为圆心, AC 长为半径画弧,交射线 B´N 于 C´ ,4 、连接 A´C´ 。斜边、直角边 (HL)斜边和一条直角边对应相等的两个直角三角形全等。判定公理有斜边和一条直角边对应相等的两个直角三角形全等 .条件 1条件 2前提结论ABCA´B´C´在 Rt△ABC 和 Rt△A´B´C´ 中∴ Rt△ABC≌Rt△A´B´C ( HL )数学表达式:{AB=A′B′AC=A′C′1. 使两个直角三角形全等的条件是( ) A. 一个锐角对应相等 B. 两个锐角对应相等 C. 一条边对应相等 D. 斜边和一条直角边对应相等2. 如图, AD⊥BE, 垂足 C 是 BE 的中点, AB=DE, 若要证△ABC≌ △DEC, 可以根据( ) A. 边边边公理 B. 斜边、直角边公理 C. 角边角公理 D. 边角边公理AEDBC当堂训练当堂训练DB3. 如图,∠ ACB =∠ADB=90 ,要证明△ ABC≌△BAD ,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。( 1 ) ( )( 2 ) ( )( 3 ) ( )( 4 ) ( )AD=BC∠DAB=∠CBABD=AC∠DBA=∠CABHL HLAASAASABDC4. 如图:...