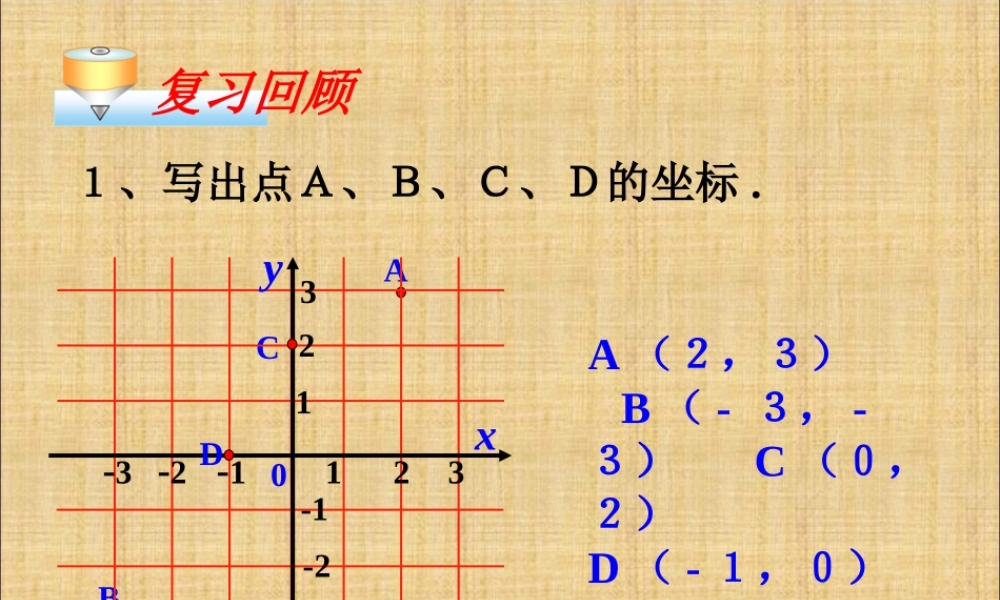
复习回顾ACB-3 -2 -1 0123 xy132-2-1-3D1、写出点A、B、C、D的坐标 .A (2,3) B ( - 3, -3) C (0,2)D ( - 1,0) 2 、下列各点分别在坐标平面的什么位置上?A ( 3 , 2 )B ( 0 ,- 2 )C (- 3 ,- 2 )D (- 3 , 0 )E (- 1.5 , 3.5 )F ( 2 ,- 3 )第一象限第三象限第二象限第四象限y 轴上x 轴上(+ , +)(- , +)(- , -)(+ , -)(0 , y)(x , 0)每个象限内的点都有自已的符号特征 .第七章 平面直角坐标系教师:吴光耀 -3 -2 -1 0123 xy132-2-1-3探究A135246-1-2-3-4-5-60E3 42-15-2-3-4-6 -560 11 、如图: 1 、将点A(-2 , -3) 向右平移 5 个单位长度,得到点 A1( , ) ; 2 、将点 A(-2 , -3) 向左平移 2 个单位长度,得到点 A2( , );A1-4-33-3 A2你发现了什么?左右平移纵坐标不变,横坐标变,变化规律是左减右加探究A135246-1-2-3-4-5-60E3 42-15-2-3-4-6 -560 13 、将点 A(-2 , -3) 向上平移 4 个单位长度,得到点 A3( , ) ;4 、将点 A(-2 , -3) 向下平移2 个单位长度,得到点A4( , ).A3A4-21-2-5你发现了什么?上下平移横坐标不变,纵坐标变,变化规律是上加下减•A1•B1•C1•A2•B2•C2 2 、将点 (x , y) 向上 ( 或下 ) 平移 b个单位长度,可以得到对应点 (x , y +b) 或 ( , ). 1 、将点 (x , y) 向右 ( 或左 ) 平移 a个单位长度,可以得到对应点(x+a , y) 或 ( , ).归纳在平面直角坐标系中,x - ayxy -b 左右平移纵坐标不变,横坐标变,变化规律是左减右加; 可以简单地理解为:例如:当 P(x , y) 向右平移 a 个单位长度,再向上平移 b 个单位长度后坐标为 p′(x+a , y+b). 上下平移横坐标不变,纵坐标变,变化规律是上加下减 .归纳1 、已知点 A ( -2 , -3 ): ( 1 )将点 A 向右平移 5 个单位长度得到点A1 ,则 点 A1 点的坐标是 ; ( 2 )将点 A 向右平移 6 个单位长度得到点A2 ,则 点 A2 点的坐标是 ; ( 3 )将点 A 向右平移 a(a>o) 个单位长度得到点 A ′ 则 点 An 点的坐标是 ; ( 4 )将点 A 向左平移 a(a>o) 个单位长度得到点 A ′ 则 点 A ′ 点的坐标是 ;( -2-a , -3 )( 3 , -3 )( 4 , -3 )( -2+ a , -3 )课堂练习2 、如图,将三角形 ABC 向左平移2 个单位长度在向下平移 3 个单位长度,则 A 、 B 、 C各点的坐标变为多少?ABC-4-51 2 3 41234-1-2-3-1-2-3oxy0A1(1, - 1)B1( - 1, -4)C1(3, - 5)ABC-4-51 2 3 41234-1-2-3-1-2-3oxy(-3 ,2)(-2 , -1)(3 ,0)3 、如图,三角形ABC 上任意一点P(x0 , y0) 经平移后得到的对应点为P1(x0+2 , y0+4) ,将三角形 ABC 作同样的平移得到三角形 A1B1C1. 求 A1 、B1 、 C1 的坐标 .P(x0, y0)P1(x0+2 , y0+4)BCB1A1C1BAC布置作业P78~79 第 3 、 4 题