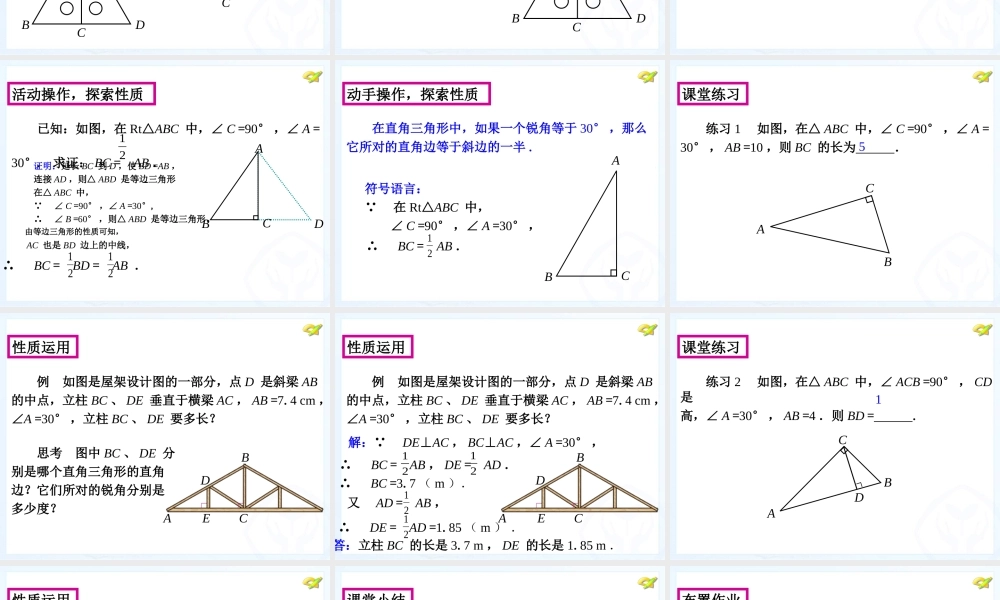
八年级 上册13.3 等腰三角形 (第 4 课时)• 学习目标: 1 .探索含 30° 角的直角三角形的性质. 2 .理解含 30° 角的直角三角形的性质,并会应用它 进行有关的证明和计算.• 学习重点: 探索并理解含 30° 角的直角三角形的性质 . 问题 已知△ ABC 中,∠ A =60°, ( ) .请你在括号内补充一个条件,使△ ABC 能成为等边三角 形 .1 、∠ B =60° 或∠ C =60°2 、 AB =BC 或 AC =BC 或 AB=AC3 、∠ B=∠C创设情境,导入新知ABC 思考 2 这个特殊的直角三角形相比一般的直角三角形有什么不同之处,它的边长有什么特殊性质?创设情境,导入新知 思考 1 等边三角形是轴对称图形,若沿着其中一 条对称轴折叠,能产生什么特殊图形? b 活动 用两个全等的含 30° 角的直角三角尺,你能拼出怎样的三角形?能拼出等边三角形吗?请说说你的理由. 活动操作,探索性质A B D C A B C D BC = AB . 12活动操作,探索性质 问题 你能借助这个图形,找到含 30° 角的直角 △ABC 的直角边 BC 与斜边 AB 之间有什么数量关系吗? A B D C 思考 这个命题是真命题吗?请进行证明. 问题 请说一说你猜想的命题中,条件和结论分别是什么?并结合图形,用符号语言表述出来 .活动操作,探索性质 猜想 在直角三角形中,如果一个锐角等于 30° ,那么它所对的直角边等于斜边的一半 .证明:延长 BC 到 D ,使 BD =AB ,连接 AD ,则△ ABD 是等边三角形在△ ABC 中, ∠ C =90° ,∠ A =30°, ∴ ∠ B =60° ,则△ ABD 是等边三角形。 已知:如图,在 Rt△ABC 中,∠ C =90° ,∠ A = 30°. 求证: BC = AB .21活动操作,探索性质ABCD AC 也是 BD 边上的中线,2121∴ BC = BD = AB . 由等边三角形的性质可知,符号语言: 在 Rt△ABC 中, ∠ C =90° ,∠ A =30° , 动手操作,探索性质 在直角三角形中,如果一个锐角等于 30° ,那么 它所对的直角边等于斜边的一半 .ABC∴ BC = AB . 215课堂练习 练习 1 如图,在△ ABC 中,∠ C =90° ,∠ A = 30° , AB =10 ,则 BC 的长为 .A B C 思考 图中 BC 、 DE 分别是哪个直角三角形的直角边?它们所对的锐角分别是多少度? 性质运用 例 如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱...