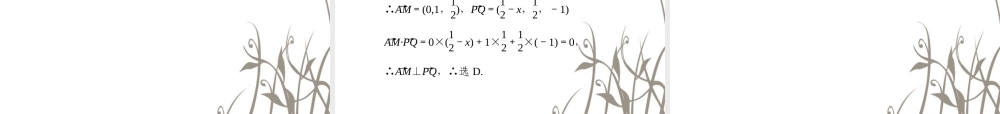理解异面直线所成的角、直线与平面所成的角、二面角的概念,会用向量方法求两条直线所成的角、线面角和二面角.重点:异面直线所成的角、线面角、二面角与向量夹角的关系.难点:如何用直线的方向向量和平面的法向量来表达线面角和二面角.1 .求异面直线所成的角设 l1 与 l2 是两异面直线, a 、 b 分别为 l1 、 l2 的方向向量, l1 、 l2 所成的角为 θ ,则〈 a , b 〉与 θ 相等或互补,∴cosθ= |a·b||a|·|b|. 2.求直线与平面所成的角 如图,设 l 为平面 α 的斜线,l∩α=A,a 为 l 的方向向量,n 为平面 α 的法向量,φ 为 l 与 α 所成的角,θ=〈a,n〉,则 sinφ=|cosθ|=|cos〈a,n〉|=|a·n||a||n|. ※ 注:由于两条直线所成的角,线面角都是锐角或直角,因此可直接通过绝对值来表达,故可直接求出,而二面角的范围是 [0 , π] ,有时比较难判断二面角是锐角还是钝角,因为不能仅仅由法向量夹角余弦的正负来判断,故这是求二面角的难点.这里给出一种简明的判断方法,供参考.3.求二面角 平面 α 与 β 相交于直线 l,平面 α 的法向量为 n1,平面 β 的法向量为 n2,=θ,则二面角 α-l-β 为 θ或 π-θ.设二面角大小为 φ,则|cosφ|=|cosθ|= |n1·n2||n1|·|n2|. 定义设平面 α 的法向量 n 在平面 α 的一侧,若向量n 的终点到平面 α 的距离小于向量 n 的起点到平面 α 的距离,则称法向量 n 指向平面 α( 如图 (1)) ;若向量 n 的终点到平面 α 的距离大于向量 n 的起点到平面 α 的距离,则称平面 α 的法向量背离平面 α( 如图 (2)) .如图,设两个平面的法向量 n1, n2在二面角 α - l -β 内,〈 n1 , n2 〉= θ ,若平面 α 的法向量 n1 指向 ( 背离 ) 平面 α ,同时平面 β 的法向量 n2 指向 ( 背离 ) 平面 β ,则二面角 α - l - β 的大小为 π - θ( 如图 (3)) ;若平面 α的法向量 n1 指向 ( 背离 ) 平面 α ,同时平面 β 的法向量 n2背离 ( 指向 ) 平面 β ,则二面角 α - l - β 的大小为 θ( 如图 (4))*3. 空间中的角包括两条异面直线所成的角、直线与平面所成的角、二面角等.这些角都是通过两条射线所成的角来定义的,因而这些角的计算方法,都是转化为平面内线与线所成的角来计算...