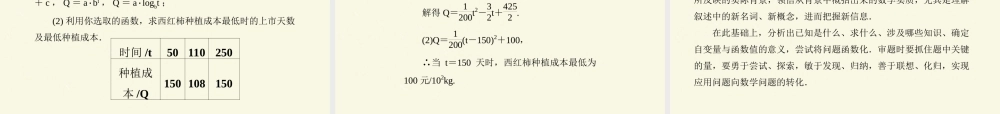3 . 2.2 函数模型的应用实例1 .几种常见的函数模型(1) 一次函数模型(2) 二次函数模型(3) 指数函数模型(4) 对数函数模型(5) 幂函数模型.1 .函数模型应用的两个方面(1) 利用已知函数模型解决问题;(2) 建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.2 .应用函数模型解决问题的基本过程数据拟合时,得到的函数为什么需要检验? 【提示】因为根据已给的数据,作出散点图,根据散点图,一般是从我们比较熟悉的、最简单的函数作模拟,但所估计的函数有时可能误差较大或不切合客观实际,此时就要再改选其他函数模型.某公司生产一种电子仪器的固定成本为 20 000 元,每生产一台仪器需增加投入 100 元,已知总收益满足函数:R(x)= 400x-12x2 (0≤x≤400)80 000 (x>400).其中 x是仪器的月产量. (1) 将利润表示为月产量的函数 f(x) ;(2) 当月产量为何值时,公司所获利润最大?最大利润为多少元?( 总收益=总成本+利润 )【思路点拨 】由题目可获取以下主要信息:①总成本=固定成本+ 100x ;②收益函数为一分段函数.解答本题可由已知总收益=总成本+利润,知利润=总收益-总成本.由于 R(x) 为分段函数,所以 f(x)也要分段求出,将问题转化为分段函数求最值问题.【解析】 (1) 设每月产量为 x 台,则总成本为 20 000 +100x ,从而 f(x) = -12x2+300x-20 000(0≤x≤400)60 000-100x(x>400). (2)当 0≤x≤400 时,f(x)=-12(x-300)2+25 000, ∴当 x=300 时,有最大值 25 000; 当 x>400 时,f(x)=60 000-100x 是减函数, f(x)<60 000-100×400<25 000. 在函数应用题中,正确理解题意,养成良好的阅读习惯是成功的一半.而二次函数模型常涉及顶点坐标、函数的单调性、区间最值等问题,二次函数的配方是比较有效的解题手段.1. 在经济学中,函数 f(x) 的边际函数 Mf(x) 定义为 Mf(x) = f(x +1) - f(x) ,某公司每月最多生产 100 件产品,生产 x(xN∈+ ) 件产品的收入函数为 R(x) = 3 000x - 20x2( 单位:元 ) ,其成本函数 C(x) =500x + 4 000( 单位:元 ) ,利润为收入与成本之差.(1) 求利润函数 P(x) 及其边际利润函数 MP(x) ;(2) 利润函数 P(x) 与边际利润函数 MP(x) 是否具有相等的最大值?【解析 】由题意知, x[1,100]∈,且 xN∈+ .(1)P(x)...