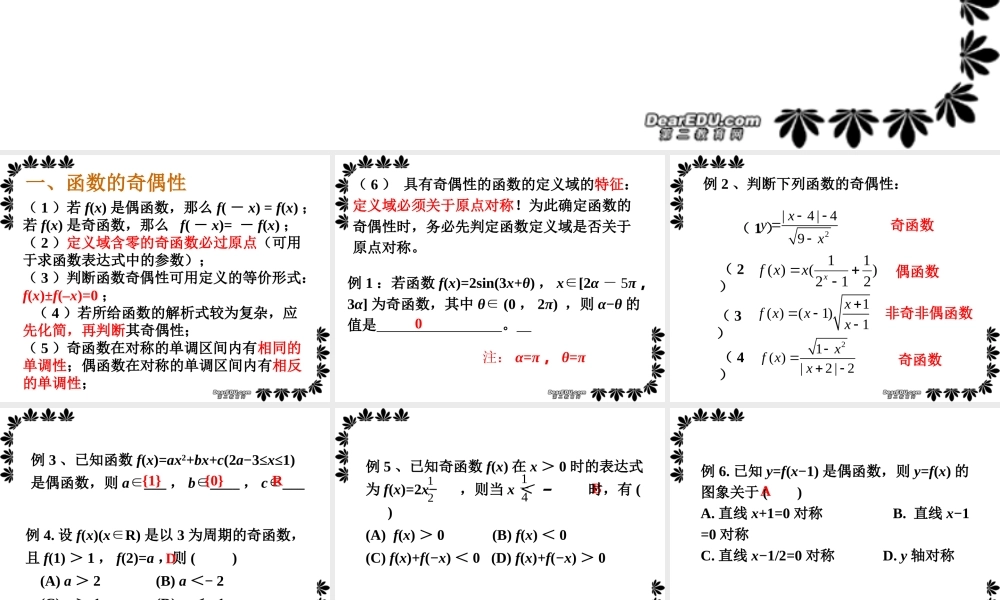
函数的性质(一)一、函数的奇偶性 ( 1 )若 f(x) 是偶函数,那么 f( - x) = f(x) ;若 f(x) 是奇函数,那么 f( - x)= - f(x) ;( 2 )定义域含零的奇函数必过原点(可用于求函数表达式中的参数);( 3 )判断函数奇偶性可用定义的等价形式:f(x)±f(–x)=0 ; ( 4 )若所给函数的解析式较为复杂,应先化简,再判断其奇偶性;( 5 )奇函数在对称的单调区间内有相同的单调性;偶函数在对称的单调区间内有相反的单调性;( 6 ) 具有奇偶性的函数的定义域的特征:定义域必须关于原点对称!为此确定函数的奇偶性时,务必先判定函数定义域是否关于原点对称。 例 1 :若函数 f(x)=2sin(3x+θ) , x[2∈α - 5π ,3α] 为奇函数,其中 θ (0∈, 2π) ,则 α−θ 的值是 。 0注: α=π , θ=π例 2 、判断下列函数的奇偶性: ( 1 ) 2|4 | 49xyx奇函数 偶函数 奇函数 非奇非偶函数 11( )()212xf xx( 2)1( )(1)1xf xxx( 3)( 4)21( )|2 | 2xf xx例 3 、已知函数 f(x)=ax2+bx+c(2a−3≤x≤1)是偶函数,则 a___∈, b____∈, c___∈{1}{0}R例 4. 设 f(x)(xR)∈是以 3 为周期的奇函数,且 f(1) > 1 , f(2)=a ,则 ( ) (A) a > 2 (B) a <− 2 (C) a > 1 (D) a <− 1 DB例 5 、已知奇函数 f(x) 在 x > 0 时的表达式为 f(x)=2x− ,则当 x < − 时,有 ( ) (A) f(x) > 0 (B) f(x) < 0 (C) f(x)+f(−x) < 0 (D) f(x)+f(−x) > 0 1214例 6. 已知 y=f(x−1) 是偶函数,则 y=f(x) 的图象关于 ( ) A. 直线 x+1=0 对称 B. 直线 x−1=0 对称 C. 直线 x−1/2=0 对称 D. y 轴对称 A2 、函数的单调性 ( 1 )一般地,设函数 f(x) 的定义域为 M :如果对于属于定义域 M 内某个区间上的任意两个自变量的值 x1 , x2 ,当 x1 < x2 时,都有 f(x1) < f(x2) ,那么就说 f(x) 在这个区间上是增函数 . 如果对于属于定义域 M 内某个区间上的任意两个自变量的值 x1 , x2 ,当 x1< x2 时,都有 f(x1) > f(x2) ,那么就说 f(x)在这个区间上是减函数 .( 2 )函数是增函数还是减函数 . 是对定义域内某个区间而言的 . 有的函数在一些区间上是增函数,而在另一些区间上可能是减函数, ...