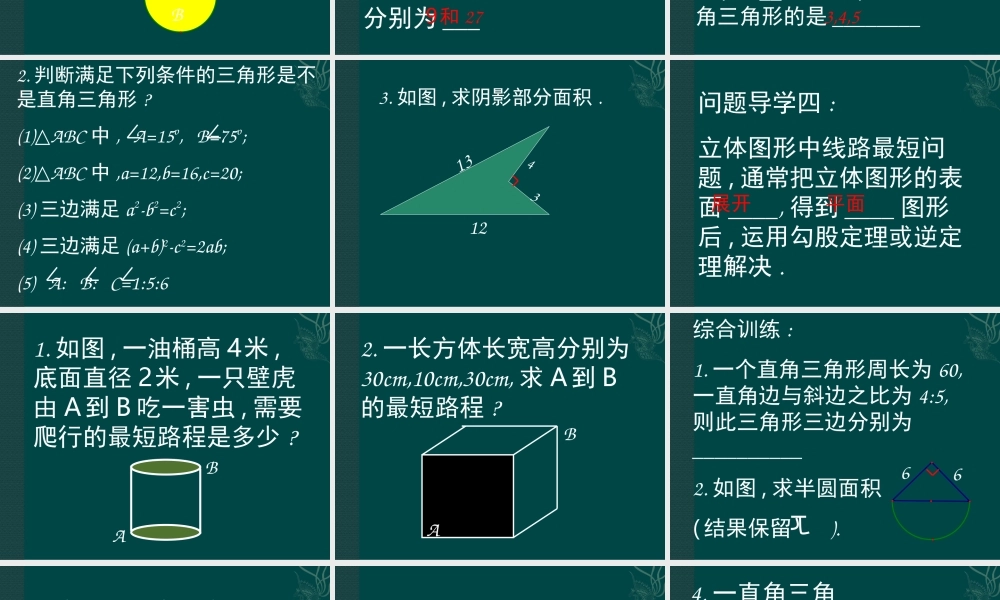
学习目标 :1. 掌握勾股定理 , 会用拼图法验证勾股定理 .2. 能应用勾股定理解决实际问题 .3. 掌握判断一个三角形是 直角三角形的条件 .问题导学 :1. 勾股定理的内容是什么 ?导学检测 :1 〉直角三角形三边长为 6,8,x, 则x=_______.2. 已知直角三角形两直角边分别为5,12, 则三边上的高的和为 ____.10 或 2 721138问题导学 :2. 你会用下面的图形验证勾股定理吗 ?abcabc1. 利用勾股定理验证三个半圆面积之间的关系ABCSA+SB=SC8102. 如图两阴影部分都是正方形 , 若它们面积之比为 1:3, 则它们的面积分别为 ___9和 27 问题导学 : 3.如果一个三角形三边为 a,b,c, 满足 _________, 则这个三角形是 直角三角形 .4. 四根长度分别为 3,4,5,6 的木棒 , 取其中三根组成三角形 , 有 __ 种取法 , 能构成直角三角形的是 ________43,4,52. 判断满足下列条件的三角形是不是直角三角形 ?(1) ABC△中 , A=15o, B=75o;(2) ABC△中 ,a=12,b=16,c=20;(3) 三边满足 a2-b2=c2;(4) 三边满足 (a+b)2-c2=2ab;(5) A: B: C=1:5:63412133. 如图 , 求阴影部分面积 .问题导学四 :立体图形中线路最短问题 , 通常把立体图形的表面 ____, 得到 ____ 图形后 , 运用勾股定理或逆定理解决 .展开平面AB1. 如图 , 一油桶高 4米 ,底面直径 2米 , 一只壁虎由 A 到 B 吃一害虫 , 需要爬行的最短路程是多少 ?AB2. 一长方体长宽高分别为30cm,10cm,30cm, 求 A 到 B的最短路程 ?综合训练 :1. 一个直角三角形周长为 60,一直角边与斜边之比为 4:5,则此三角形三边分别为__________2. 如图 , 求半圆面积( 结果保留 ).66AB3. 如图 , 两个正方形面积分别为 64,49, 则AB=______一架云梯长 25 米 , 斜靠在一面墙上 , 梯子底端离墙 7米 , 如果梯子顶端下滑 4米 , 则梯子底部在水平方向上滑动几米 ?ACDBE4. 一直角三角形纸片直角边AC=6,BC=8, 现将直角边 AC沿 AD 折叠 ,使 C与 E 重合 , 则CD=____.5. 折叠矩形的一边 AD, 使点D 落在点 F 处 , 已知AB=8cm,BC=10cm, 求 EC.BACDEF