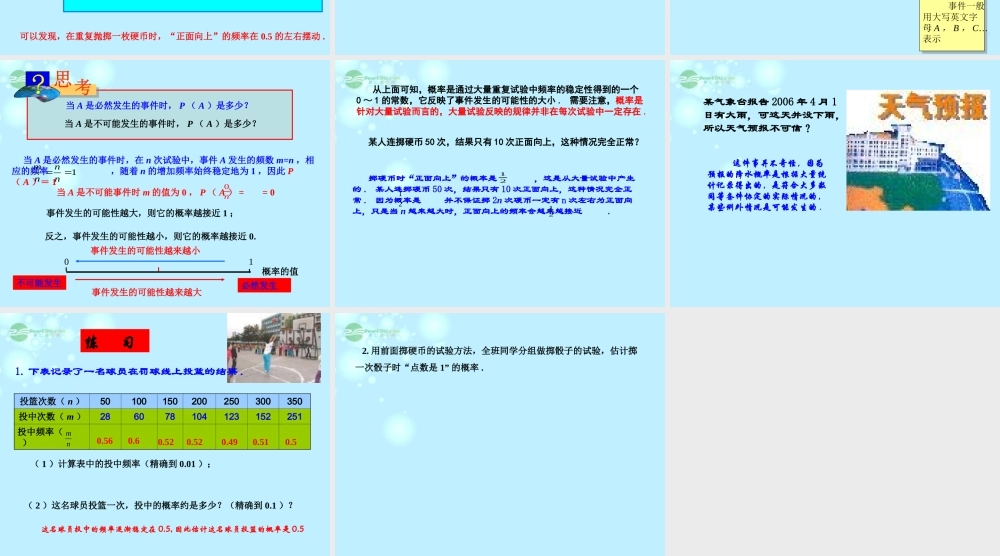
在同样条件下,随机事件可能发生也可能不发生,那么,它发生的可能性究竟有多大?这是我们下面要讨论的问题 . 问题:凭直觉你认为:正面朝上与反面朝上的可能性是多少?我们从抛掷硬币这个简单问题说起 . 直觉告诉我们这两个事件发生的可能性各占一半 . 这种猜想是否正确,我们用试验来进行验证: 把全班同学分成 10 组,每组同学掷一枚硬币 50 次,整理同学们获得的试验数据,并记录在表中 . 第一组的数据填在第一列,第一、二组的数据之和在第二列,…, 10 个组的数据之和填在第 10 列 . “ 正面向上”的频率“ 正面向上”的频数 m50045040035030025020015010050抛掷次数 nnm根据上表中的数据,在图中标注出对应的点 . 0.5150 100 150 200300400 450250350500“ 正面向上”的频率nm请同学们根据试验所得数据想一想:“正面向上”的频率有什么规律?使用帮助使用帮助历史上,有些人曾做过成千上万次抛掷硬币的试验,他们的试验结果见表试验者抛掷次数( n )“ 正面向上”次数( m )“ 正面向上”频率( )莫弗204810610.518布丰404020480.5069费勒1000049790.4979皮尔逊1200060190.5016皮尔逊24000120120.5005nm随着抛掷次数的增加,“正面向上”的频率的变化趋势有何规律?可以发现,在重复抛掷一枚硬币时,“正面向上”的频率在 0.5 的左右摆动 . 可以发现,在重复抛掷一枚硬币时,“正面向上”的频率在 0.5 的左右摆动 . 随着抛掷次数的增加,一般地,频率就呈现出一定的稳定性:在 0.5 的左右摆动的幅度会越来越小 . 由于“正面向上”的频率呈现出上述稳定性,我们就用 0.5 这个常数表示“正面向上”发生的可能性的大小 . 在抛掷一枚硬币时,结果不是“正面向上”就是“反面向上”,因此,从上面提到的试验中也能得到相应“反面向上”的频率 . 当“正面向上”的频率逐渐稳定到 0.5 时,“反面向上”的频率呈现什么规律吗?容易看出,“反面向上”的频率也相应地稳定到 0.5 ,于是我们也用 0.5 这个常数表示“反面向上”发生的可能性的大小,至此,试验验证了我们的猜想:抛掷一枚质地均匀的硬币时,“正面向上”与“反面向上”的可能性相等(各占一半) . 因为在 n 次试验中,事件 A 发生的频数 m 满足 0≤m≤n ,所以,进而可知频率 所稳定到的常数 p 满足 0≤p≤1 ,因此 0≤P(A) ≤1nm10 nm上面我们用随机事件发生的频率逐渐稳定到的常数刻画了随...