数学 2.2.2 双曲线的简单几何性质课件 新人教A版选修1-1 课件VIP免费

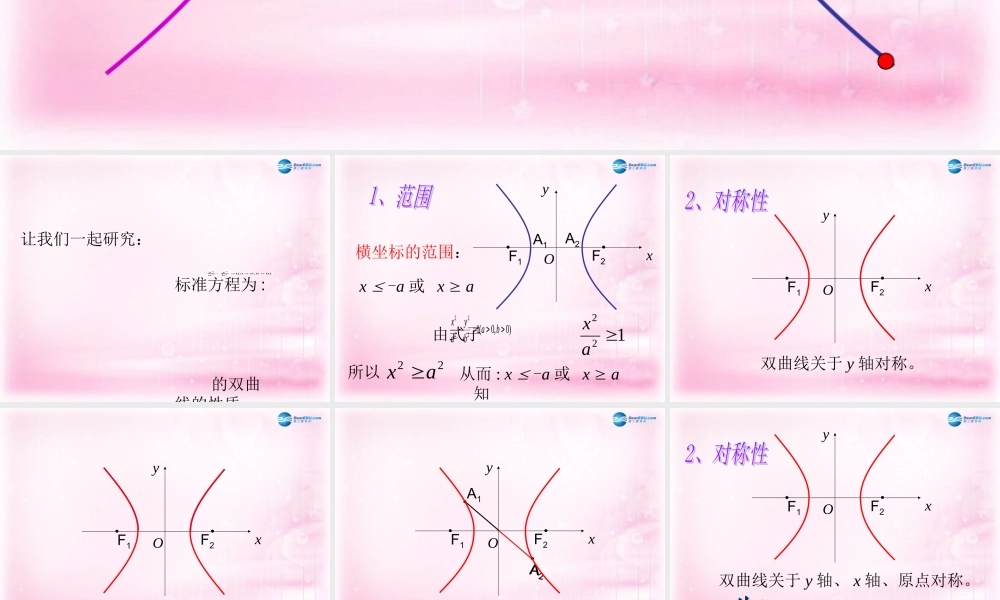
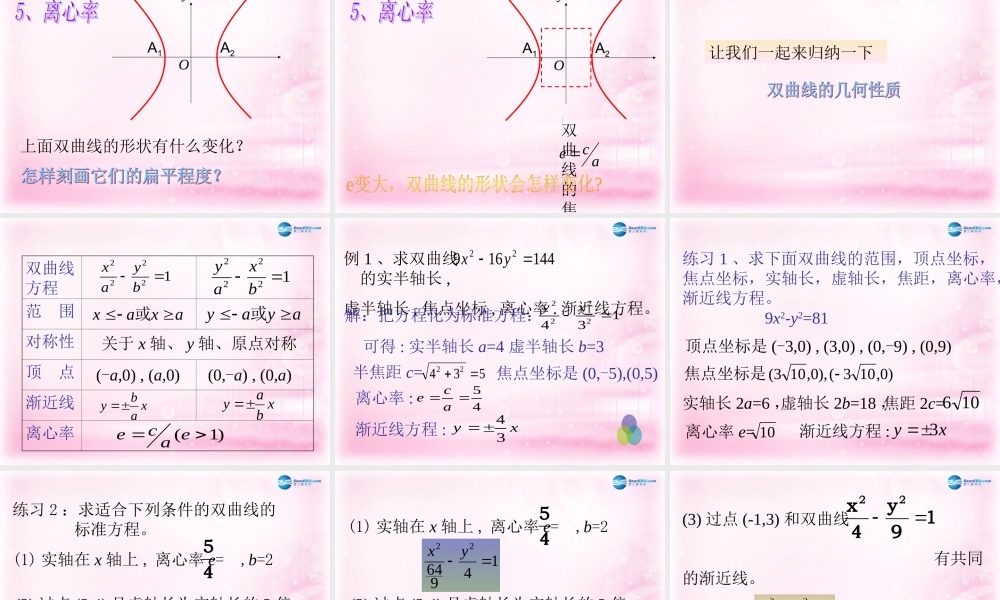
2.2.2 让我们一起研究：标准方程为 : 的双曲线的性质。)0,0(12222babyax F2F1OA1A2xy横坐标的范围：从而 : x  -a 或 x  a由式子 知)0,0(12222babyax x  -a 或 x  a122ax所以 22ax  F2F1Oxy双曲线关于 y 轴对称。 F2F1Oxy双曲线关于 x 轴对称。 A2A1A2F2F1Oxy双曲线关于原点对称。 F2F1Oxy双曲线关于 y 轴、 x 轴、原点对称。 OB2B1A1A2xy可得 x=  a从而： A1(-a,0),A2(a,0)也把 B1(0, -b),B2(0, b) 画在 y 轴上在 中令y=0 ，12222byax为双曲线的顶点 OB2B1A1A2xy线段 A1A2 叫双曲线的实轴 ;线段 B1B2 叫双曲线的虚轴。长为 2a长为 2b OB2B1A1A2xy红色虚框的两条对角线，为双曲线的 渐近线abxaby其方程为 一般结论：02222 byax)0(2222byax双曲线 的渐近线为 149)1(22 yx 194)2(22 yx 1188)3(22 yx 1818)4(22 yx 练习 1 、计算下列双曲线的渐近线：你能发现什么规律吗？ 12222byax在方程 中，如果a=b,那么，虚线方框是正方形，并且实轴等于虚轴。OB2B1A1A2y实轴和虚轴等长的双曲线叫 等轴双曲线。 上面双曲线的形状有什么变化？OA1A2y 双曲线的焦距与长轴长的比 称为双曲线的离心率，用e表示，即acace OA1A2y 让我们一起来归纳一下 双曲线方程范 围对称性 顶 点 渐近线离心率 12222 byax12222 bxayxabyxbayaxax或ayay或)1( eace关于 x 轴、 y 轴、原点对称(-a,0) , (a,0)(0,-a) , (0,a) 例 1 、求双曲线 的实半轴长 ,虚半轴长 , 焦点坐标 , 离心率 . 渐近线方程。14416922yx解：把方程化为标准方程：1342222 xy可得 : 实半轴长 a=4 虚半轴长 b=353422半焦距 c=焦点坐标是 (0,-5),(0,5)离心率 :45ace渐近线方程 :xy34 练习 1 、求下面双曲线的范围，顶点坐标，焦点坐标，实轴长，虚轴长，焦距，离心率，渐近线方程。 9x2-y2=81焦点坐标是顶点坐标是 (-3,0) , (3,0) , (0,-9) , (0,9)实轴长 2a=6 ，虚轴长 2b=18 ，焦距 2c=离心率 e=渐近线方程 :106)0,103(),0,103(10xy3 练习 2 ：求适合下列条件的双曲线的 标准方程。(1) 实轴在 x 轴上 , 离心率 e= ,b=24519y4x22(3) 过点 (-1,3) 和双曲线 有共同的渐近线。 (2) 过点 (3,4) 且虚轴长为实...