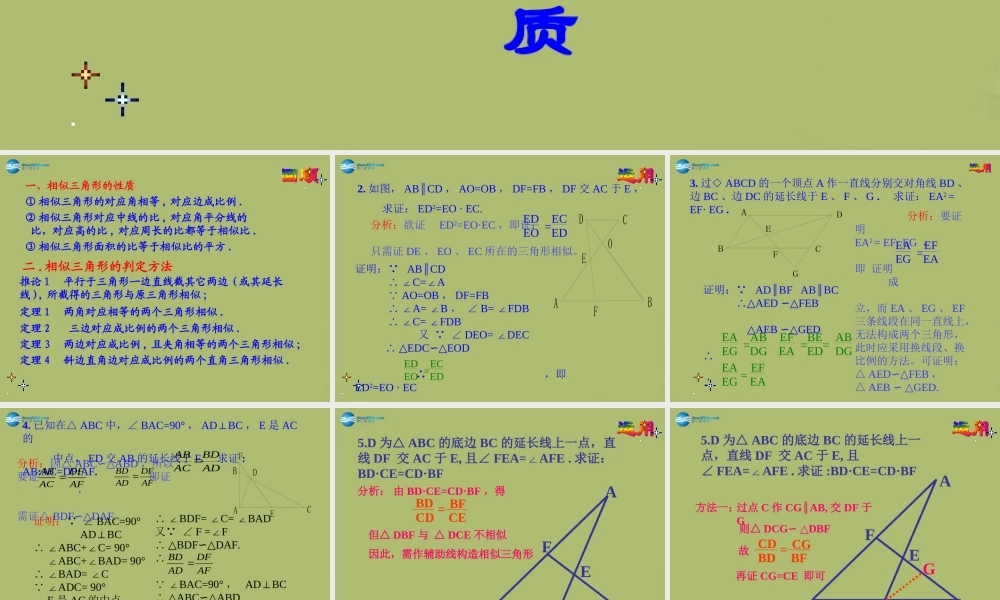
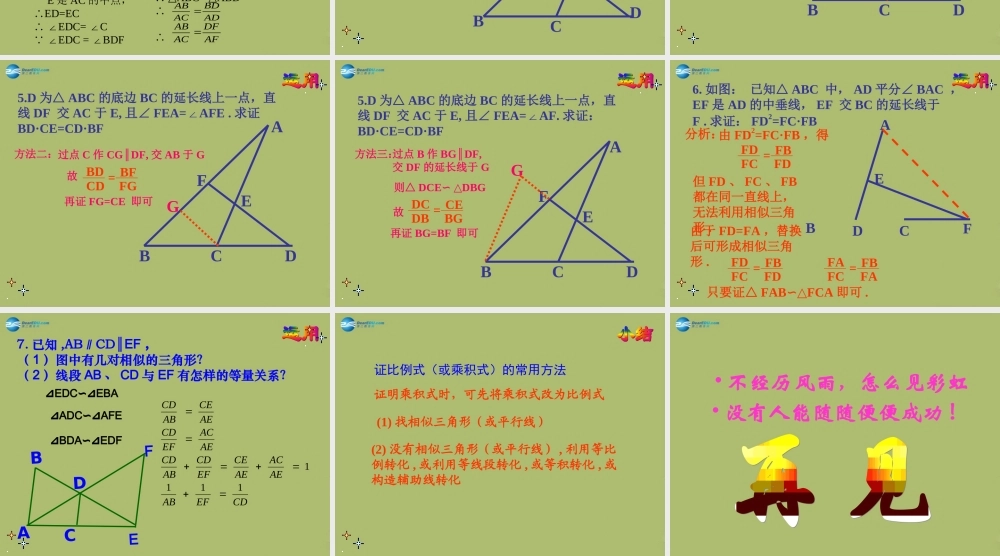
相似三角形的性质一、相似三角形的性质① 相似三角形的对应角相等 , 对应边成比例 .② 相似三角形对应中线的比 , 对应角平分线的 比,对应高的比 , 对应周长的比都等于相似比 .③ 相似三角形面积的比等于相似比的平方 .二 . 相似三角形的判定方法定理 1 两角对应相等的两个三角形相似 .推论 1 平行于三角形一边直线截其它两边 ( 或其延长线 ), 所截得的三角形与原三角形相似 ;定理 2 三边对应成比例的两个三角形相似 .定理 3 两边对应成比例 , 且夹角相等的两个三角形相似 ;定理 4 斜边直角边对应成比例的两个直角三角形相似 .2. 如图, AB CD∥, AO=OB , DF=FB , DF 交 AC 于 E , 求证: ED2=EO · EC.ABCDEFO分析:欲证 ED2=EO·EC ,即证:只需证 DE 、 EO 、 EC 所在的三角形相似。EDEO =ECED 证明: AB CD∥ ∴ ∠C=A∠ AO=OB , DF=FB ∴ ∠A= B∠, ∠ B= FDB∠ ∴ ∠C= FDB∠ 又 ∠ DEO= DEC∠ ∴ △EDCEOD∽△ ∴ ,即 ED2=EO · ECEDEO =ECED 3. 过◇ ABCD 的一个顶点 A 作一直线分别交对角线 BD 、边 BC 、边 DC 的延长线于 E 、 F 、 G . 求证: EA2 = EF· EG .ABCDEFG 分析:要证明 EA2 = EF· EG ,即 证明 成立,而 EA 、 EG 、 EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△ AEDFEB∽△, △ AEB GED.∽ △证明: AD BF AB BC∥∥ ∴△AED FEB ∽△ △AEB GED∽△∴∴EAEG =ABDG EFEA =BEED= ABDG EAEG = EFEA EAEG =EFEA 4. 已知在△ ABC 中,∠ BAC=90° , ADBC⊥, E 是 AC的 中点, ED 交 AB 的延长线于 F. 求证 : AB:AC=DF:AF.ADEFBC分析:因△ ABCABD∽△,所以要证 即证 ,需证△ BDFDAF.∽△AFDFACAB ADBDACAB AFDFADBD 证明: ∠ BAC=90° ADBC⊥ ∴ ∠ABC+C= 90°∠ ∠ABC+BAD= 90°∠ ∴ ∠BAD= C∠ ∠ADC= 90° E 是 AC 的中点,∴ED=EC ∴ ∠EDC= C∠ ∠EDC = BDF∠AFDFADBD ∴ ∠BDF= C= BAD∠∠又 ∠ F =F∠ ∴ △BDFDAF.∽△∴ ∠BAC=90° , ADBC⊥ ∴ △ABCABD ∽△∴∴ADBDACAB AFDFACAB 5.D 为△ ABC 的底边 BC 的延长线上一点,直线 DF 交 AC 于 E, 且∠ FEA=AFE ...