广东省高二数学选修2-1 双曲线的标准方程课件 苏教版 课件VIP免费

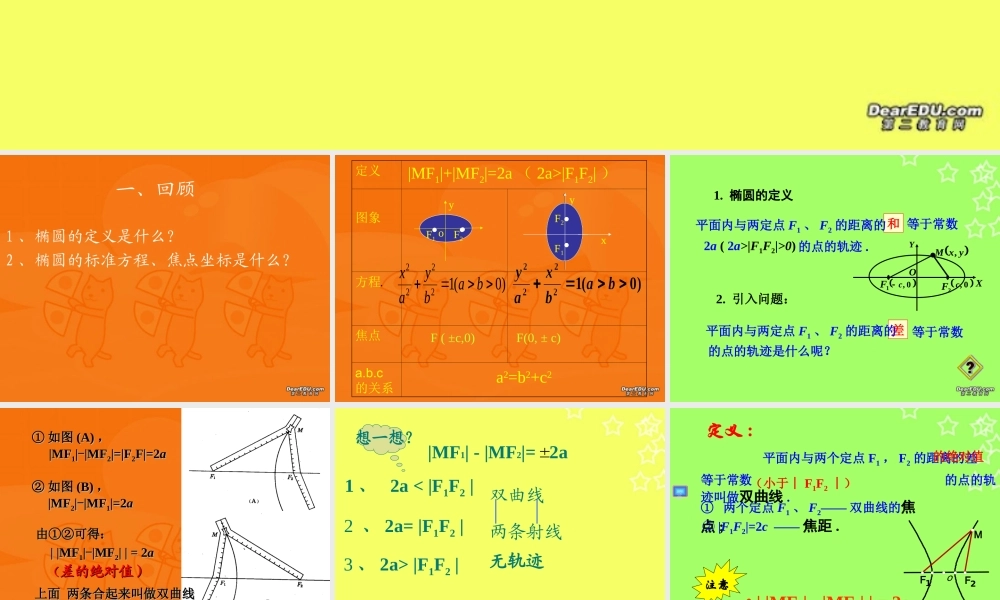
双曲线的标准方程2.3.1一、回顾1 、椭圆的定义是什么？ 2 、椭圆的标准方程、焦点坐标是什么？定义图象方程焦点a.b.c的关系y·oxF1F2··yoF1F2· ·|MF1|+|MF2|=2a （ 2a>|F1F2| ）a2=b2+c2F ( ±c,0) F(0, ± c) oF1F2···)0(12222babyax1. 椭圆的定义和 等于常数2a ( 2a>|F1F2|>0) 的点的轨迹 .平面内与两定点 F1 、 F2 的距离的1F2F0,c0,cXYOyxM,2. 引入问题：差 等于常数的点的轨迹是什么呢？平面内与两定点 F1 、 F2 的距离的①① 如图如图 (A)(A) ，， |MF|MF11||--|MF|MF22|=|F|=|F22F|=2F|=2aa②② 如图如图 (B)(B) ，，|MF|MF22||--|MF|MF11|=2|=2aa上面 两条合起来叫做双曲线上面 两条合起来叫做双曲线由①②可得：由①②可得： | |MF| |MF11||--|MF|MF22| | = 2| | = 2a a （（差的绝对值）差的绝对值） 双曲线两条射线1 、 2a < |F1F2 | 2 、 2a= |F1F2 | 3 、 2a> |F1F2 | 无轨迹|MF1| - |MF2|= 2a想一想？① 两个定点 F1 、 F2—— 双曲线的焦点 ; ② |F1F2|=2c —— 焦距 .oF2F1M 平面内与两个定点 F1 ， F2 的距离的差等于常数 的点的轨迹叫做双曲线 .动画的绝对值（小于︱ F1F2 ︱）注意定义 :• | |MF1| - |MF2| | = 2a1. 建系设点 .F2F1MxOy2. 写出适合条件的点 M 的集合；3. 用坐标表示条件，列出方程；4. 化简 .求曲线方程的步骤：方程的推导xyo 设 M （ x , y ） , 双曲线的焦距为 2c （ c>0 ） ,F1(-c,0),F2(c,0)常数 =2aF1F2M即 (x+c)2 + y2 - (x-c)2 + y2 = + 2a_ 以 F1,F2 所在的直线为 X 轴，线段 F1F2 的中点为原点建立直角坐标系1. 建系 .2. 设点．3. 列式．|MF1| - |MF2|= 2a,,如何求这优美的曲线的方程？4. 化简 .aycxycx2)()(2222222222)(2)(ycxaycx222)(ycxaacx)()(22222222acayaxacoF2FMyx1222bac)0,0(12222babyaxF1F2yxoy2a2 -x2b2= 1焦点在 y 轴上的双曲线的标准方程• 想一想12222 byax12222 bxayF2F1MxOyOMF2F1xy)00(ba，双曲线的标准方程问题：如何判断双曲线的焦点在哪个轴上？问题：如何判断双曲线的焦点在哪个轴上？练习：写出以下双曲线的焦点坐标练习：写出以下双曲线的焦点坐标1916.122 yx1916.322 xy1169.222...