等差数列求和1VIP免费

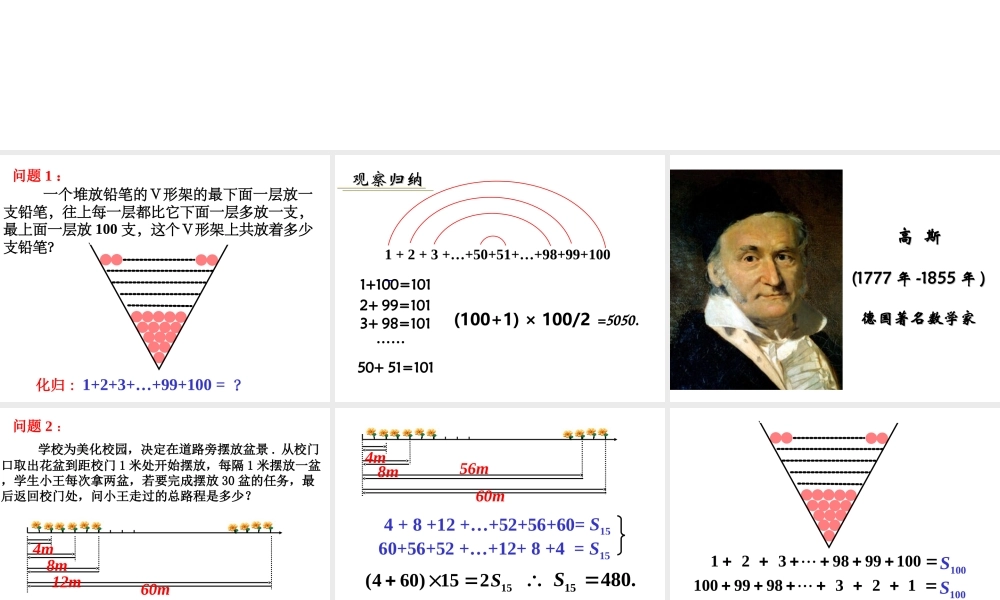
2.3.1 等差数列的前 n 项和(1) 一个堆放铅笔的Ｖ形架的最下面一层放一支铅笔，往上每一层都比它下面一层多放一支，最上面一层放 100 支，这个Ｖ形架上共放着多少支铅笔？ 化归 : 1+2+3+…+99+100 = ？ 问题 1 ：1 + 2 + 3 +…+50+51+…+98+99+100 1+100=101 2+ 99=101 3+ 98=101 …… 50+ 51=101 (100+1) × 100/2观察归纳观察归纳=5050.高 斯高 斯(1777(1777 年年 -1855-1855 年年 ))德国著名数学家德国著名数学家 学校为美化校园，决定在道路旁摆放盆景 . 从校门口取出花盆到距校门 1 米处开始摆放，每隔 1 米摆放一盆，学生小王每次拿两盆，若要完成摆放 30 盆的任务，最后返回校门处，问小王走过的总路程是多少？问题 2 ：4m 8m12m60m化归 : 4+8+12+…+60= ？ 4 + 8 +12 +…+52+56+60= ？ 15(460) 152S15480.S60+56+52 +…+12+ 8 +4 = ？ 答：小王走过的总路程是 480 米 . 4m 8m56m60mS15S151239899100?1009998321?100(1100) 1002S5050 .S100S100 如图，工地有上一堆圆木，从上到下每层的数目分别为 1 ， 2 ， 3 ，……， 10 。问共有多少根圆木？请用简便的方法计算。设等差数列 {an} 的前 n 项和为 Sn , 即： Sn= a1 + a2 + a3 +… + an-2 + an-1 + anSn= an + an-1+ an-2 +… + a3 + a2 + a1两式相加得 : 2Sn = (a1+an )×n12132......nnnaaaaaa2)( 1nnaanS1.1. 公式推导公式推导算法：算法：倒序相加倒序相加法法() ... [(1) ]nnnnSaadand111()...[(1) ]nSaadand12()nnSn aa两式相加得 :1() 12nnn aaS公式：1(1)naand1(1)22nn nSnad公式 ：推导公式 ( 教材 ) ：前 n 和公式：共 5 个量，由三个公式联系，知三可求二 . 通项公式：1() 12nnn aaS公式：1(1)22nn nSnad公式 ：1(1)naand 例 1 、计 算： （ 1 ） 1+2+3+…+n = ________. （ 2 ） 1+3+5+…+(2n-1) =________ . （ 3 ） 2+4+6+…+2n =__________ .(1)2n n 2n(1)n n 例 2 等差数列 -10 ， -6 ， -2 ， 2 ， … 前多少项的和为 54 ？解：设题中的等差数列是｛ an ｝，前 n 项和为 Sn则 a1 ＝－ 10 ， d ＝－ 6 －（...