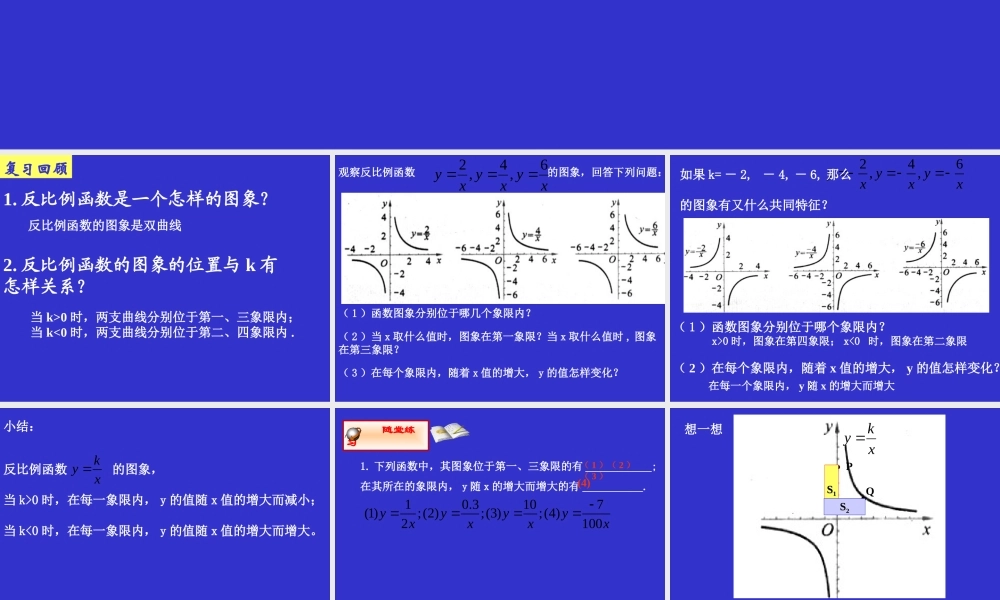
第二节 反比例函数的图象与性质(二) 第五章 反比例函数 复习回顾1. 反比例函数是一个怎样的图象? 2. 反比例函数的图象的位置与 k 有怎样关系?当 k>0 时,两支曲线分别位于第一、三象限内;当 k<0 时,两支曲线分别位于第二、四象限内 .反比例函数的图象是双曲线 观察反比例函数 的图象,回答下列问题:xyxyxy6,4,2( 1 )函数图象分别位于哪几个象限内?( 2 )当 x 取什么值时,图象在第一象限?当 x 取什么值时 , 图象在第三象限?( 3 )在每个象限内,随着 x 值的增大, y 的值怎样变化? 246,,yyyxxx如果 k= - 2, - 4, - 6, 那么的图象有又什么共同特征?( 1 )函数图象分别位于哪个象限内? x>0 时,图象在第四象限; x<0 时,图象在第二象限( 2 )在每个象限内,随着 x 值的增大, y 的值怎样变化?在每一个象限内, y 随 x 的增大而增大 反比例函数 的图象,当 k>0 时,在每一象限内, y 的值随 x 值的增大而减小;当 k<0 时,在每一象限内, y 的值随 x 值的增大而增大。kyx小结: 随堂练习1. 下列函数中,其图象位于第一、三象限的有 ____________;在其所在的象限内, y 随 x 的增大而增大的有 ___________.10.3107(1);(2);(3);(4)2100yyyyxxxx( 1 )( 2 )( 3 )(4) PQSS11SS22S1 、 S2 有什么关系?为什么?想一想xky 观察反比例函数图象的两支曲线 , 回答下列问题 : (1) 它们会与坐标轴相交吗? ( 2 )反比例函数的图象是轴对称图形吗? ( 3 )反比例函数的图象是中心对称图形吗?它们都不与坐标轴相交。是轴对称图形 , 它们有两条对称轴 .是中心对称图形 , 对称中心是坐标原点 . 已知反比例函数 ,y 随 x 的增大而减小,求 a 的值和表达式 .271aayax 补充练习:210(1)71(2)12,31(aaaaaaa解: 依题意得:由(1)得:由(2)得:舍去)1的值为2, 反比例函数为y=x 习题 5.31. 下列函数中,其图象位于第一、三象限的有 __________;在其所在的象限内, y 随 x 的增大而增大的有 ___________.20.158(1);(2);(3);(4)3300yyyyxxxx2. 已知点 A(-2,y1),B(-1,y2),C(3,y3) 都在反比例函数 的图象上,比较 y1 、 y2 、 y3 的大小关系。4yx解:∵ k=4>0 ∴ 图象在第一、三象限内,每一象限内 y 随 x 的增大而减小 ∵x10, ∴ 点 A(-2,y1) ,点 B(-1,y2) 在第三象限点 C(3,y3) 在第一象限。∴y3>0, y2