人教版高二数学双曲线方程 课件VIP免费

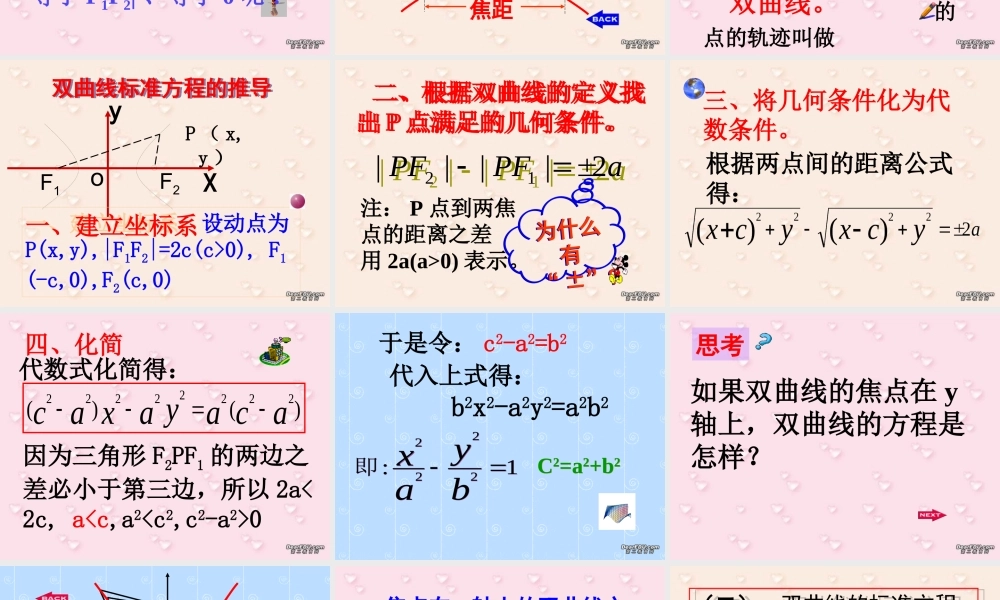
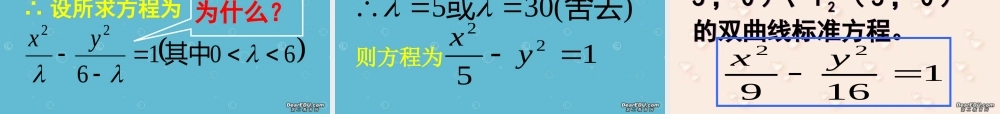1 、求曲线方程的步骤1 、求曲线方程的步骤一、建立坐标系，设出相关点及动点的坐标；二、找出动点满足的几何条件；三、将几何条件化为代数条件；四、化简，得所求方程、说明。[ 复习 ][ 复习 ] 2 、椭圆的定义 2 、椭圆的定义到平面上两定点 F1 ， F2 的距离之和（大于 |F1F2| ）为常数的点的轨迹叫椭圆。aPFPF2213 、椭圆标准方程有几类3 、椭圆标准方程有几类[ 两类 ])(12222轴上焦点在xbyax)(12222轴上焦点在yaybx 到平面上两定点 F1 ， F2 的距离之差（小于 |F1F2| ）为非零常数的点的轨迹是什么 ? 问题 1问题 1画画看画画看问题 2问题 2 常数等于 F1F2| 、等于 0 呢 ? 双曲线的画法： 双曲线的画法：焦点焦点焦距 定义： 到平面上两定点 F1 、 F2 的距离 的绝对值（小于|F1F2| ）为 的点的轨迹叫做之差 非零常数双曲线。（一）、双曲线的定义（一）、双曲线的定义双曲线标准方程的推导双曲线标准方程的推导уF1F2χoP （ x,y ）一、建立坐标系；设动点为P(x,y),|F1F2|=2c(c>0), F1(-c,0),F2(c,0)一、建立坐标系注： P 点到两焦点的距离之差用 2a(a>0) 表示。 二、根据双曲线的定义找出 P 点满足的几何条件。 二、根据双曲线的定义找出 P 点满足的几何条件。aPFPF2||||12aPFPF2||||12为什么有“ ±”?为什么有“ ±”?三、将几何条件化为代数条件。根据两点间的距离公式得：四、化简代数式化简得：)()(22222222acayaxac因为三角形 F2PF1 的两边之差必小于第三边，所以 2a<2c, a0于是令： c2-a2=b2 代入上式得： b2x2-a2y2=a2b2 1:2222 byax即1:2222 byax即C2=a2+b2C2=a2+b2思考如果双曲线的焦点在 y轴上，双曲线的方程是怎样？12222 bxay12222 bxayC2=a2+b2C2=a2+b2焦点在 y 轴上的双曲线方程焦点在 y 轴上的双曲线方程（二）、双曲线的标准方程（二）、双曲线的标准方程12222 byax12222 byax12222 bxay12222 bxay c2=a2+b2 c2=a2+b212222 byax12222 byax12222 bxay12222 bxayC2=a2+b2yyxx[ 例题 1] 判断下列各双曲线方程焦点所在的坐标轴；求 a 、 b 、 c 各为多少？[ 例题 1] 判断下列各双曲线方程焦点所在的坐标轴；求 a 、 b 、 c 各为多少？11625)1(22 yx3694)2(22 yx194)2(22 xy194)2(22 xy...