姜晓儒演示文稿VIP免费

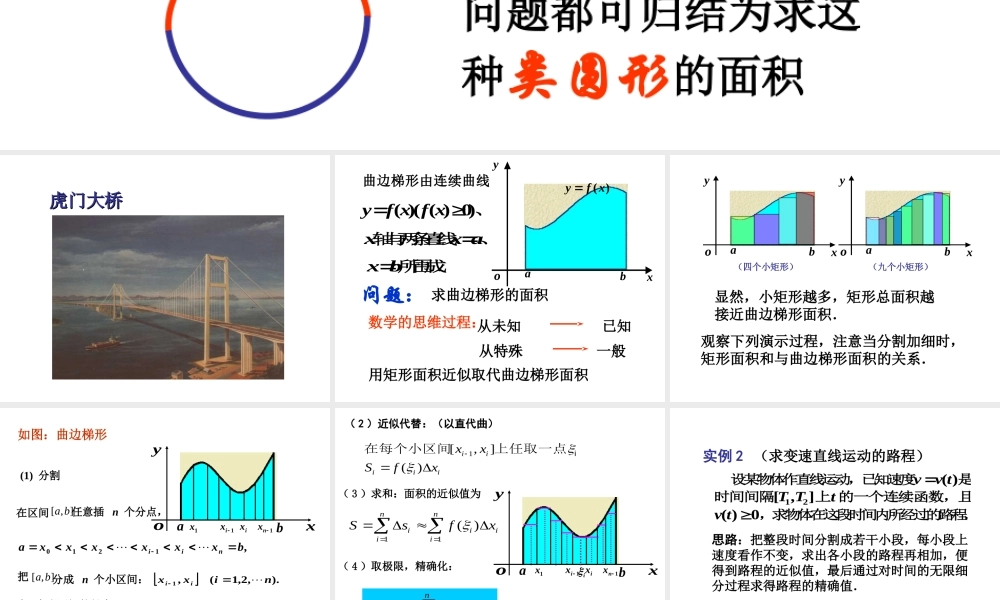
一、问题的提出实例 1 （求曲边梯形的面积） 求面积问题由来已久，对于由直线所围成的平面图形的面积我们已经会求，下图所示的图形如何求面积大量的工程技术实际问题都可归结为求这种类圆形的面积一、定积分的概念 虎门大桥虎门大桥 曲边梯形由连续曲线 )(xfy)0)((xf、 x轴与两条直线 ax、 bx所围成.abxyo)(xfy 问题： 求曲边梯形的面积数学的思维过程：从未知 已知从特殊 一般用矩形面积近似取代曲边梯形面积 abxyo（四个小矩形）abxyo（九个小矩形）显然，小矩形越多，矩形总面积越接近曲边梯形面积．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系． abxyoix1x1ix1nx,1210bxxxxxxanii(1) 分割).,2,1(1nixxxiii 在区间 ],[ba任意插 n 个分点，把],[ba分成 n 个小区间： ).,2,1( ,1nixxii每 个小区间的长度如图：曲边梯形 abxyoiix1x1ix1nx（ 3 ）求和：面积的近似值为11()nniiiiiSsfx（ 2 ）近似代替：（以直代曲）1[,]()iiiiixxSfxi在每个小区间上任取一点（ 4 ）取极限，精确化：01lim()niixiSfx  实例 2 （求变速直线运动的路程） 设某物体作直线运动，已知速度)(tvv是时间间隔],[21 TT上t 的一个连续函数，且0)(tv，求物体在这段时间内所经过的路程.思路：把整段时间分割成若干小段，每小段上速度看作不变，求出各小段的路程再相加，便得到路程的近似值，最后通过对时间的无限细分过程求得路程的精确值． 路程 = 速度 × 时间 .匀速直线运动：t1T2T0t1t2t1itit1ntnti(1) 分割,21101TtttttTnii(2) 近似代替iiitvs)(  iniiniitvss11(3) 求和},{max1init(4) 取极限.)(lim10niiitvs 1iiittt),,2,1(ni（求变速直线运动的路程）实例 2 从上面例子看出，不管是求曲边梯形的面积或是计算变速运动的路程，它们都归结为对问题的某些量进行“分割、近似代替、求和、取极限”，或者说都归结为形如 的和式极限问题。我们把这些问题从具体的问题中抽象出来，作为一个数学概念提出来就是今天要讲的定积分。由此我们可以给定积分的定义。 niixif1)( 设函数)(xf 在],[ba上有界，记},,,max{21nxxx， 如果不论对],[ba在],[ba中任意插入...