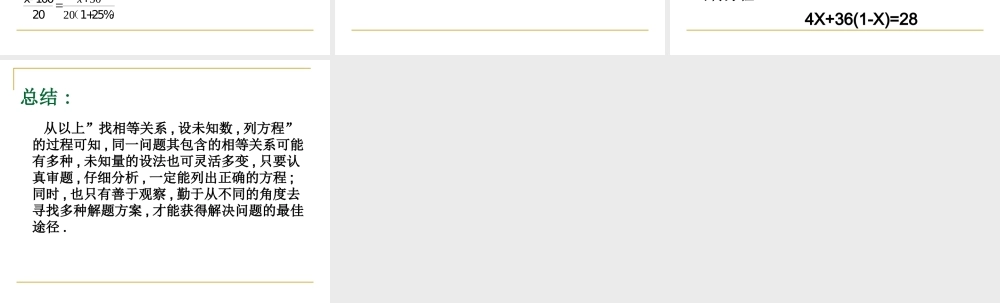
如何找相等关系 列方程解应用题是初中数学的一个重点 , 也是一个难点 , 要突破这一个难关 , 学会寻找相等关系是关键 , 那么怎样寻找应用题中的相等关系呢 ?(1)要善于分析问题中的不变量,并利用不变量来列方程.(2)要善于用不同的方法表示同一个量,由此得到相等关系,从而列出方程.(3)要善于利用”总量等于各个分量之和”列方程. (1) 要善于分析问题中的不变量 , 并利用不变量来列方程 .例如 : 一艘船航行于 A,B 两个码头之间 , 顺水航行需 3 小时 , 逆水航行需 5 小时 , 已知水流速度是 4 千米 / 时 , 求这两个码头之间的距离 .分析 1: 很明显 , 这两个码头之间的距离是不变量 , 可根据此列方程 . 为此 , 设船在静水中速度为 X 千米 / 时 , 则船顺水航行速度为 (X+4) 千米 / 时 , 逆水航行的速度为 (X-4) 千米 / 时 , 由不变量得方程 : 3(X+4)=5(X-4) 例如 : 一艘船航行于 A,B 两个码头之间 , 顺水航行需 3 小时 , 逆水航行需 5 小时 , 已知水流速度是 4 千米 / 时 , 求这两个码头之间的距离 .分析 2: 不难看出 , 船在静水中的速度也是不变量 ,可根据此列方程 . 为此 , 设 A,B 两码头之间的距离为 X 千米 , 则船顺水航行时速度为 x/3 千米 /时 , 逆水航行速度为 X/5 千米 / 时 , 由不变量得方程 : x/3 - 4= X/5 +4 (2) 要善于用不同的方法表示同一个量 , 由此得到相等关系 , 从而列出方程 .例如 : 某工人按原计划每天生产 20 个零件 , 到预定期限还有 100 个零件不能完成 , 若提高工作效率 25%, 到期将超额完成 50 个 , 问此工人原计划生产零件多少个 ? 预定期限是多少天 ?50205020Xxx解析一:设原计划生产零件 个,则预定期限可用代数式x-100表示为或天,20(1+25%)于是有方程:x-10020(1+25%) 例如 : 某工人按原计划每天生产 20 个零件 ,到预定期限还有 100 个零件不能完成 , 若提高工作效率 25%, 到期将超额完成 50 个 , 问此工人原计划生产零件多少个 ? 预定期限是多少天 ?解析二 : 设预定期限为 X 天 , 则提高工作效率后完成的零件数可分别表示为 20(1+25%)X或 20X+100+50, 从而可建立方程 : 20X·25%=100+50 (3) 要善于利用”总量等于各个分量之和”列方程 .例如 : 某中学师生到离校 28 千米的地方郊游 , 开始的一段路是步行 , 步行...