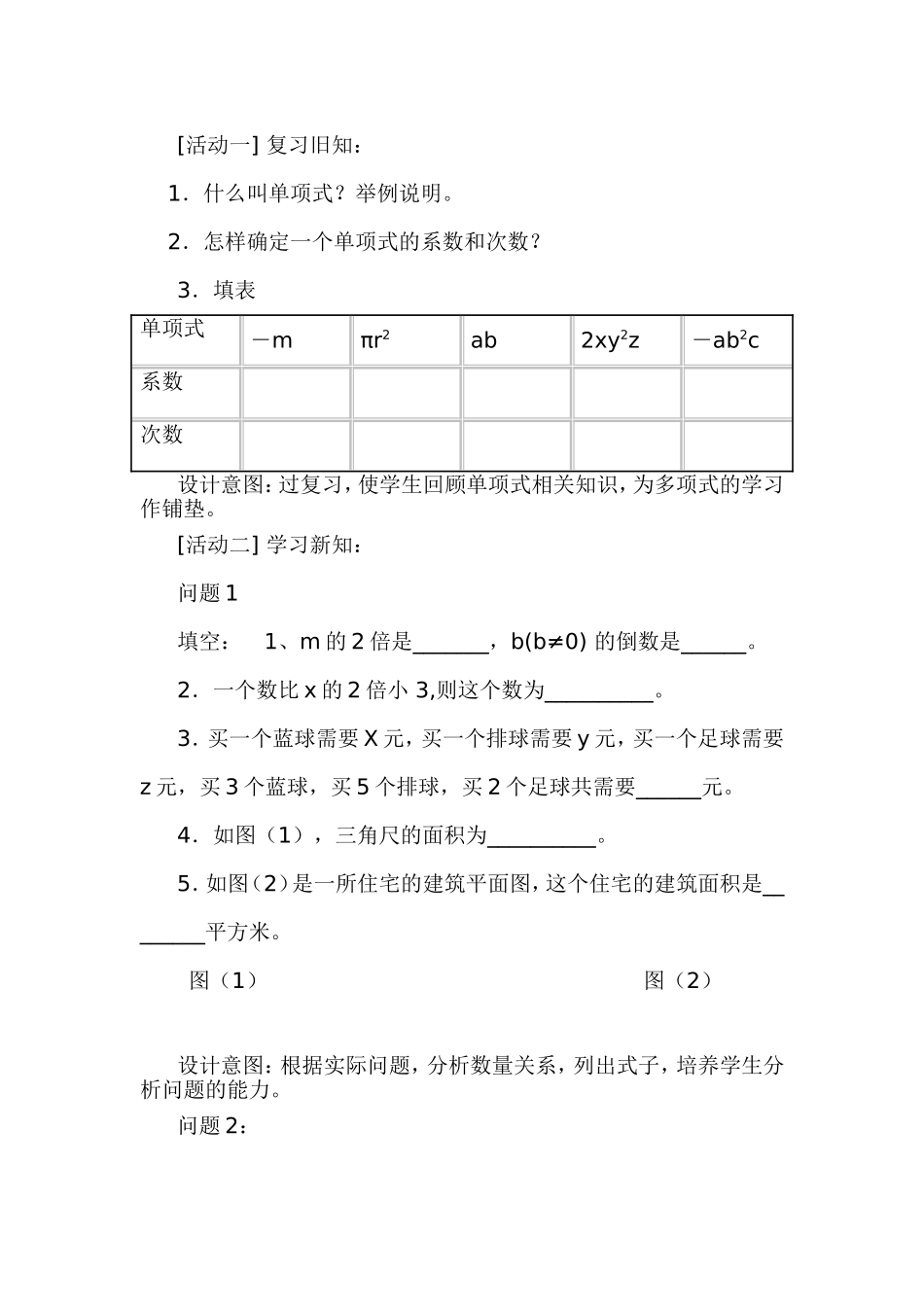
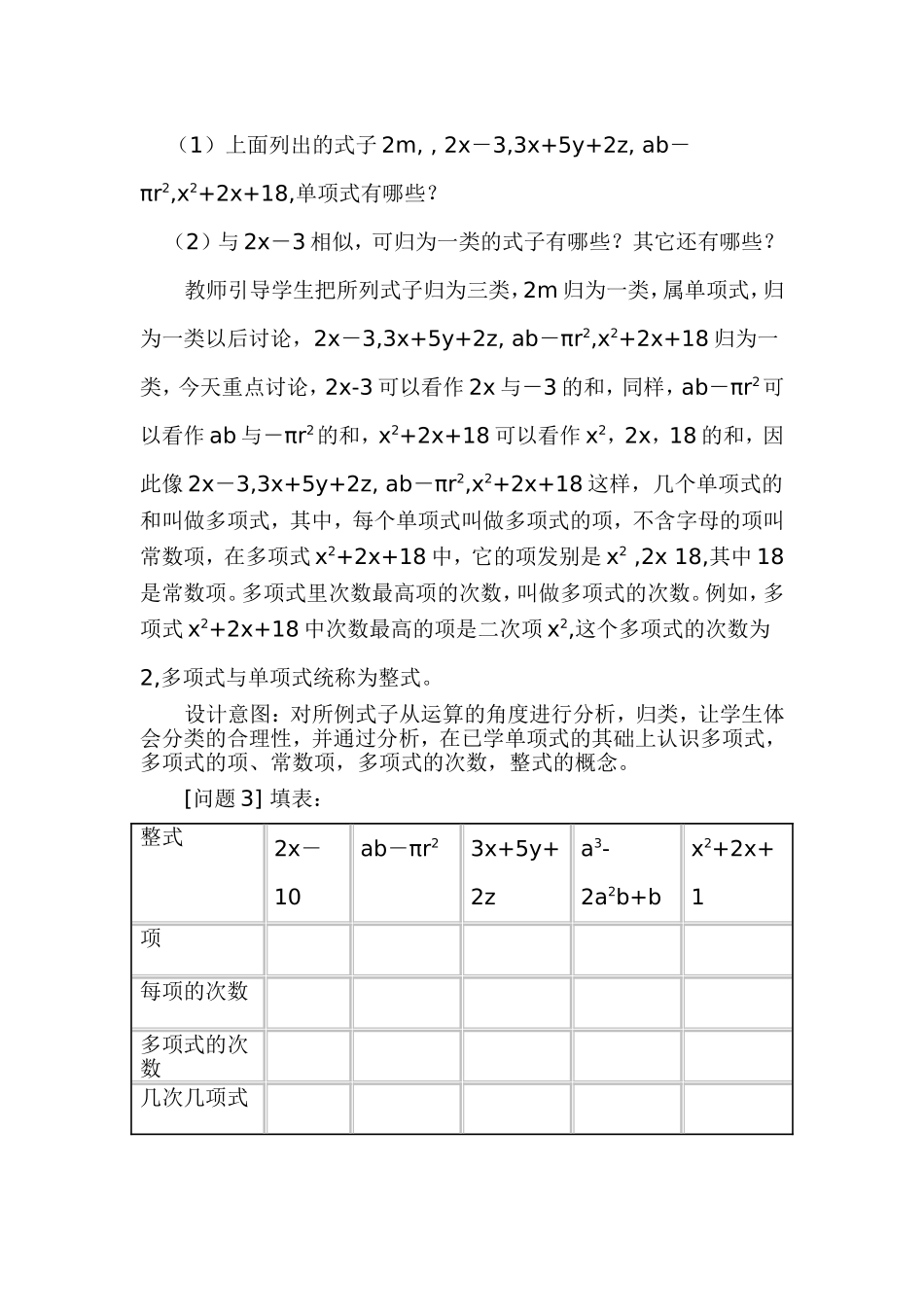
多项式的教学设计教学目标:1.使学生理解多项式,整式的概念,会准确确定一个多项式的项数和次数。2.能用多项式表示具体问题中的数量关系。3.通过实例列整式,培养学生分析问题、解决问题的能力。4.通过对式子的分类,体会数学定义的合理性和必要性。教学重点: 1.理解掌握多项式的项、常数项、次数的概念。2.用多项式表示具体问题中的数量关系。教学难点:准确确定多项式的次数和项。教学关键:掌握单项和多项式次数之间的区别和联系。内容分析:教材中,首先给出思考题:课本 P56 (1)、 (2)、 (3)、 (4),然后得出式子 2x-3 , 3x+5y+2z, ab-πr2,x2+2x+18.然后对这些式子进行分析,指出它们的特点,从而归纳出多项式的意义,研究上列代数式时,着重指出,上列式子都是几个单项式的和,如 2x-3,是 2x 与-3 的和,由此可知,这里的“+”是省略了,而每一个单项式都带有前面的符号,有正号,也有负号,教学时,对上述特点结合实例加以强调,使学生得到一个深刻的印象。接着,教材中指出多项式、多项式的项,常数项的概念,随后研究多项式的次数,由于多项式的每一项(单项式)都有次数,在比较多项式中各项次数的大小的基础上,引出多项式次数概念,多项式次数是多项式中次数最高项的次数。单项式,多项式都有次数。教学中,要使学生弄清它们之间的联系和区别。最后,教材中安排例 2、例 3,并提出“单项式与多项式统称整式”。教学过程:[活动一] 复习旧知: 1.什么叫单项式?举例说明。 2.怎样确定一个单项式的系数和次数?3.填表单项式-mπr2ab2xy2z-ab2c系数 次数 设计意图:过复习,使学生回顾单项式相关知识,为多项式的学习作铺垫。[活动二] 学习新知:问题 1填空: 1、m 的 2 倍是_______,b(b≠0) 的倒数是______。2.一个数比 x 的 2 倍小 3,则这个数为__________。3.买一个蓝球需要 X 元,买一个排球需要 y 元,买一个足球需要z 元,买 3 个蓝球,买 5 个排球,买 2 个足球共需要______元。4.如图(1),三角尺的面积为__________。5.如图(2)是一所住宅的建筑平面图,这个住宅的建筑面积是________平方米。 图(1) 图(2) 设计意图:根据实际问题,分析数量关系,列出式子,培养学生分析问题的能力。问题 2:(1)上面列出的式子 2m, , 2x-3,3x+5y+2z, ab-πr2,x2+2x+18,单项式有哪些?(2)与 2x-3 相似,可归为一类的式子有哪些?其它还有哪些?教师引导学...