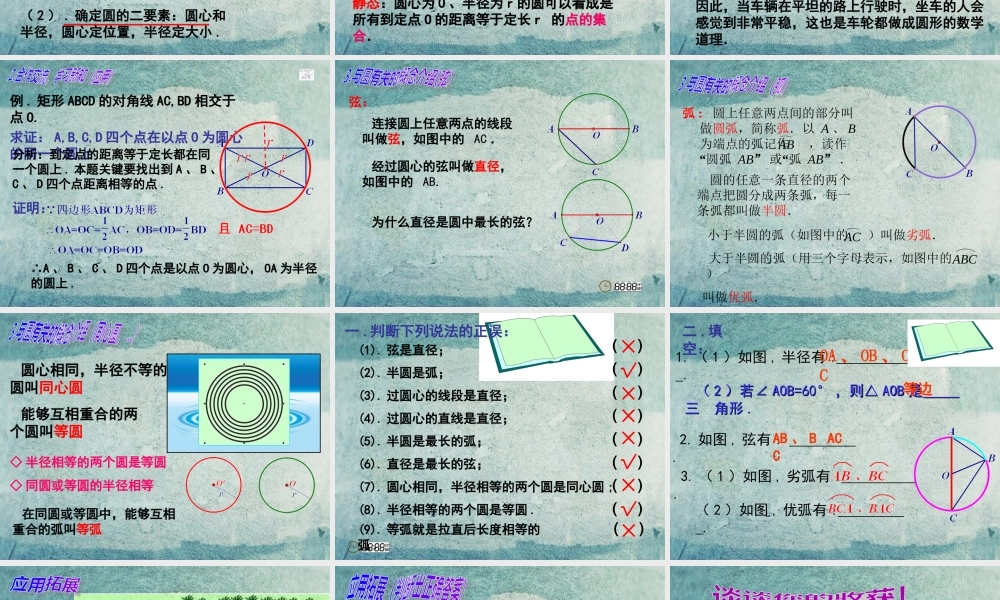
1. 经历圆的概念的形成过程,理解圆、弧、弦等与圆有关的概念;2. 获取根据圆的定义来证明点共圆的基本方法,能解决简单的实际问题,增强应用意识;4. 提高学习过程中 的“动手操作”能力,培养合作学习的意识和对知识探索精神 .3. 体会圆在生产、生活中的广泛应用,感受数学的价值;4. 提高学习过程中 的“动手操作”能力,培养合作学习的意识和对知识探索精神 . 圆是一种基本的几何图形,圆形在生活中随处可见,观察下列图形从中找出共同特点 仿照并选取一种方法画圆,观察画圆的过程,你能说出圆的形成过程吗?OA 在一个平面内,线段 OA 绕它固定的一个端点 O旋转一周,另一个端点 A 所形成的图形叫做圆.固定的端点 O 叫做圆心,线段 OA 叫做半径 以点 O 为圆心的圆,记作“⊙ O” ,读作“圆 O” .由圆的定义知:( 1 ) .“ 圆”指的是“圆周”,即一条封闭的曲线 .( 2 ) . 确定圆的二要素:圆心和半径,圆心定位置,半径定大小 .圆的概念OA动态:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.静态:圆心为 O 、半径为 r 的圆可以看成是所有到定点 O 的距离等于定长 r 的点的集合.静态:圆心为 O 、半径为 r 的圆可以看成是所有到定点 O 的距离等于定长 r 的点的集合. 我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于半径. 我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于半径. 把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变;因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.例 . 矩形 ABCD 的对角线 AC,BD 相交于点 O.求证: A,B,C,D 四个点在以点 O 为圆心的同一个圆上 .分析:到定点的距离等于定长都在同一个圆上 . 本题关键要找出到 A 、 B 、C 、 D 四个点距离相等的点 .证明:∴A 、 B 、 C 、 D 四个点是以点 O 为圆心, OA 为半径的圆上 . 经过圆心的弦叫做直径,如图中的 AB. 连接圆上任意两点的线段叫做弦,如图中的 AC .弦: 为什么直径是圆中最长的弦? 圆的任意一条直径的两个端...