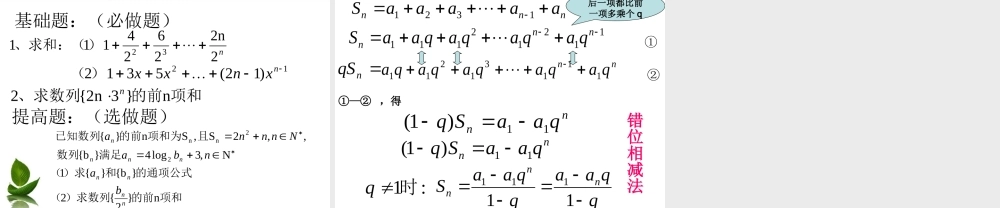数列求和(错位相减法-)VIP免费

数列求和 专题普通高中人教版 数学 必修五-———— 错位相减法黄娜音 复习回顾前面，我们学习了数列求和的哪些方法？1 、公式法：等差数列的前 n 项和公式：naadnnnan2S2)1(S1n1n或等比数列的前 n 项和公式：1n11nS1,q11)1(S1,qnaqqaaqqann当当 前面，我们学习了数列求和的哪些方法？2 、分组求和法：通项公式是“等差 等比”型数列的求和复习回顾注： 在求和之前，一定要先判断数列的类型，如何判断？通项公式：一次函数等差数列指数型函数等比数列 项和的前求数列项和的前求数列项和的前求数列的通项公式为数列，的通项公式为已知数列例题：n}{)3(n}b{)2(n}{)1(2b}b{}{nnnnnnnnnbaanaa方法探究等差数列等比数列公式法分组求和法新问题：求数列 的前 n 项和}{nnba？ N 年后，如果你自己开了公司，当了老板，但是由于资金短缺，需向银行贷款1000 万。银行向你推荐了一个新的贷款方案：情景重现： 银行一次性借给你 1000 万元，你可以分 30个月偿还，第一个月还 2 元，第二个月还 4 元，第三个月还 8 元，第四个月还 10 元，以此类推，每个月的还款数是前一个月的两倍。你能接受这个方案吗？银行贷款问题 302S即30S请同学们考虑如何求出这个和？302S).2222(23032313022  S元2147483646223130S错位相减法 !30302SS作减法等比数列的前等比数列的前 nn 项项和和30322222情景重现：3143222223122 后一项都比前一项多乘个 2 方法探究项和的前新问题：求数列的通项公式，数列的通项公式例：数列n}{2b}b{}{nnnnnnnbanaannnnnnnnnbababanba22)1(2221SS212n2211n即解：①-② 得nS2132221)-n(2221nnn132n22222Snnn即132n221212121Snnn22)1(22122211nnnnn1n2)1(2Snn故错位相减法：展开，乘公比，错位，相减 nnnnnnaa2b}b{}{的通项公式数列，的通项公式例：数列变式训练变式问题：求数列 的前 n 项和}{nnba 课堂练习nnnnnnnnnnnnnnnnnnnnnnnnTnnTnnnba)21()21(2T21)21(1)21(21121)21(21)21()21()21(21)21(21121121121)21()21()1()21(2)21(121)21()21()1()21(2211T)21(n21n11121n213212n...