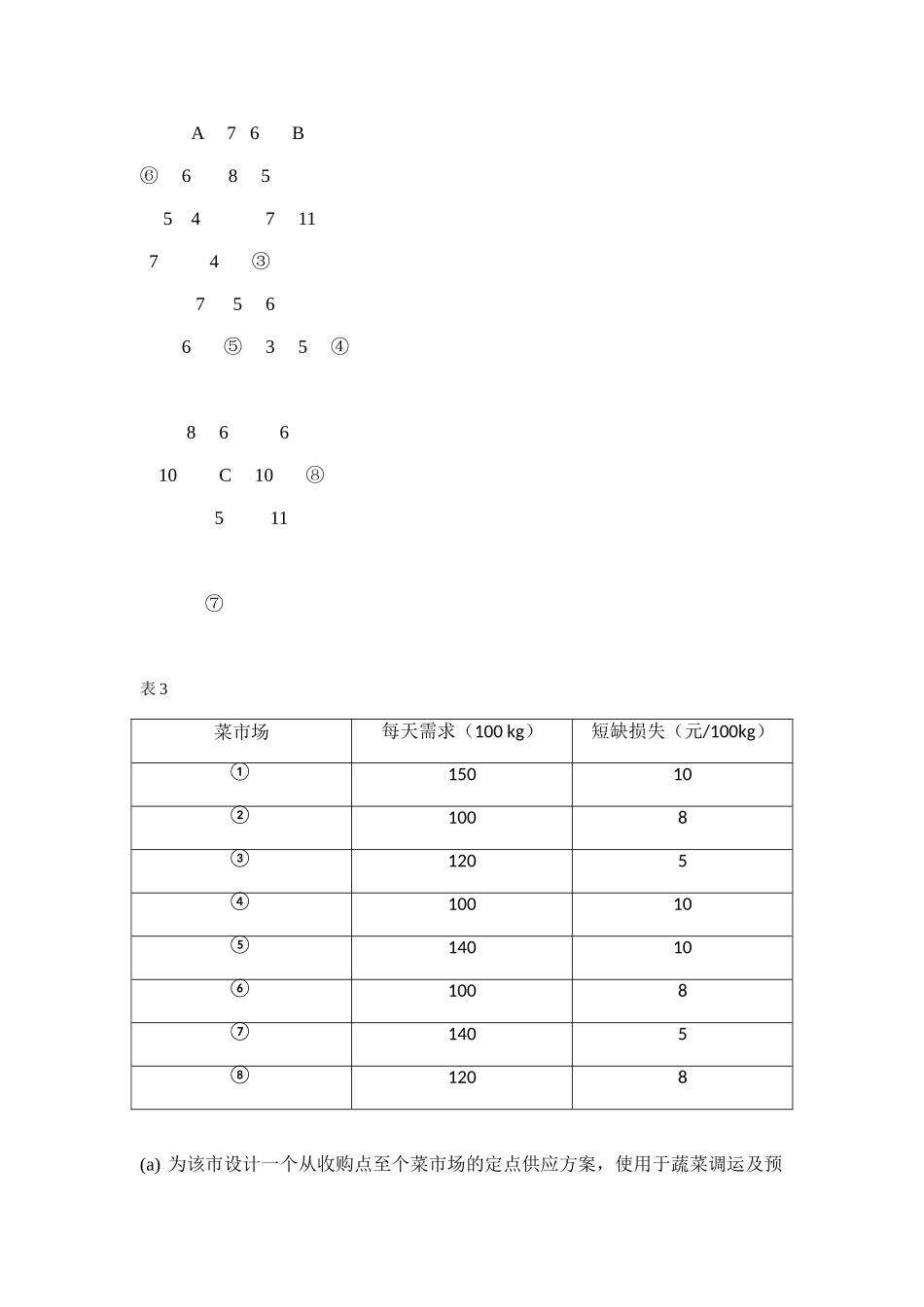
光明市的菜篮子工程摘要本文研究的是蔬菜市场为满足不同条件的最优调配方案问题,用了 Froyd算法、线性规划建立了一系列数学规划模型,并用 MATLAB 和 LINGO 软件编程实现。关于问题一:用 Froyd 算法结合 MATLAB 编程求出收购点至个菜市场的最短距离,以用于蔬菜调运及预期的短缺损失为最小为目标建立线性规划模型。用LINGO 编程求得日均费用最少为 4610 元。关于问题二:在模型一的基础增加各菜市场短缺量一律不超过需求量的20%的约束条件,用 LINGO 编程求得最少日均费用以及最优供应方案。费用最少为 4806 元,供应方安见正文。 关于问题三:在模型一的基础上,改为以供货充足、费用最小为目标,建立模型三,用 LINGO 编程求得日均费用为 4770 元,增产的蔬菜每天应分给 C 收购点 8000Kg。关键字:蔬菜市场调配方案 Froyd 算法 线性规划一、问题的重述海江市是一个人口不到 20 万人的小城市。根据该市的蔬菜种植情况,分别在菜市场(A),菜市场(B)和菜市场(C)设三个收购点,再由各收购点分送到全市的 8 个菜市场,该市道路情况,各路段距离(单位:100m)及各收购点,菜市场①⑧的具体位置见图 3.2.按常年情况,A,B,C 三个收购点每天收购量分别为 30000,25000 和 20000(单位:100 kg),各菜市场的每天需求量及发生供应短缺时带来的损失(元/100kg)见表 3.设从收购点至各菜市场蔬菜调运费为 1 元/(100kg.100m).① 7 ②5 4 8 3 7 A 7 6 B⑥ 6 8 5 5 4 7 11 7 4 ③ 7 5 6 6 ⑤ 3 5 ④ 8 6 6 10 C 10 ⑧ 5 11 ⑦表 3菜市场每天需求(100 kg)短缺损失(元/100kg)①15010②1008③1205④10010⑤14010⑥1008⑦1405⑧1208(a) 为该市设计一个从收购点至个菜市场的定点供应方案,使用于蔬菜调运及预期的短缺损失为最小;(b) 若规定各菜市场短缺量一律不超过需求量的 20%,重新设计定点供应方案;(c) 为满足城市居民的蔬菜供应,光明市的领导规划增加蔬菜种植面积,试问增产的蔬菜每天应分别向 A,B,C 三个采购点供应多少最经济合理。二、 符号说明 从 A 到 i(各个菜市场)的最短距离 从 B 到 i(各个菜市场)的最短距离 从 C 到 i(各个菜市场)的最短距离 从 A 到 i(各个菜市场)的运货量 从 B 到 i(各个菜市场)的运货量 从 C 到 i(各个菜市场)的运货量 总调运费 短缺损失 总费用三 模型假设1、假设日需求量与缺货...