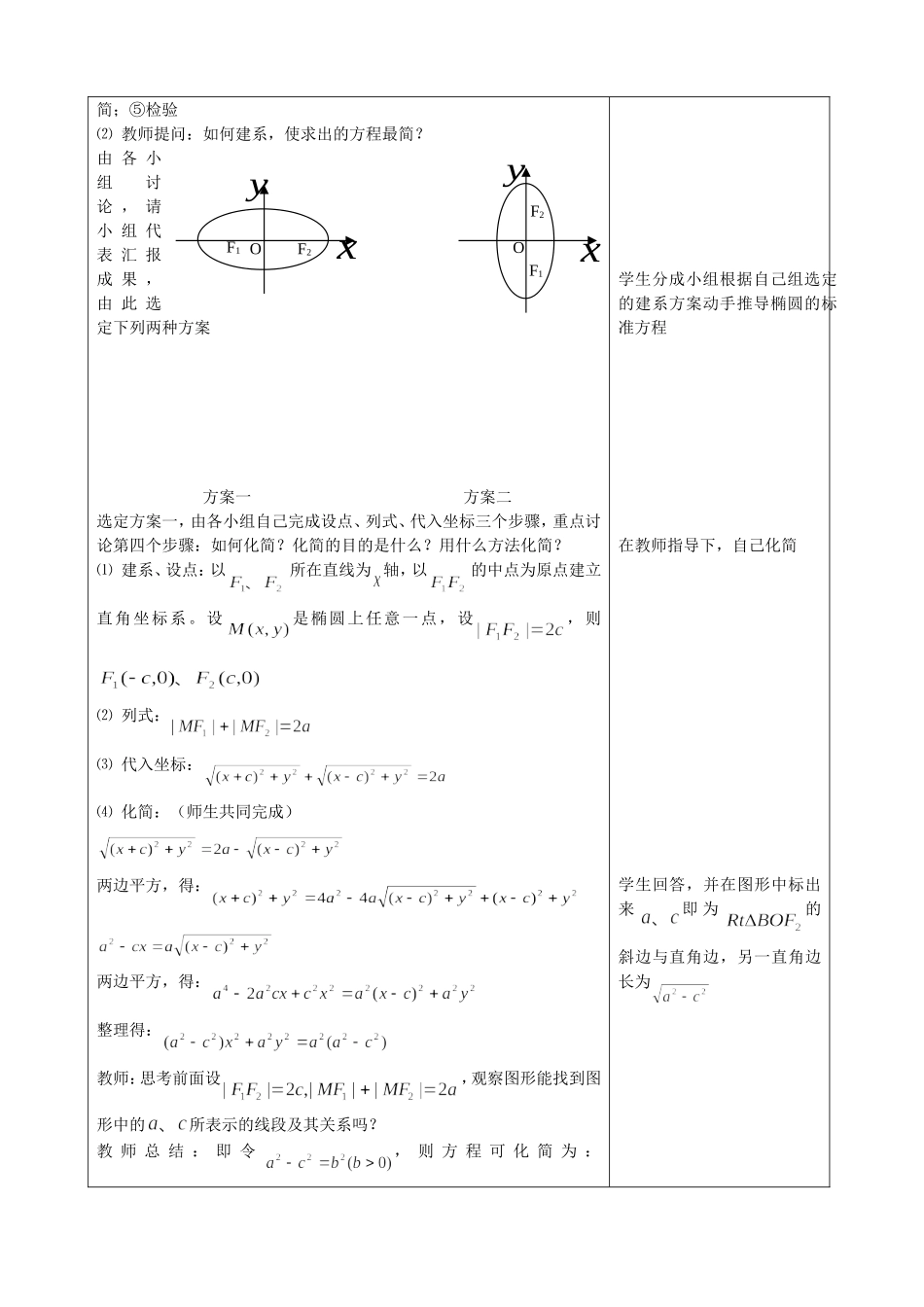
椭圆及其标准方程教学设计黑龙江省实验中学数学组:曾庆占2009 年 5 月 4 日课题椭圆及其标准方程的教学设计教师曾庆占职称中教一级教龄9 年学校黑龙江省实验中学课型新课教学目知识与技能⑴ 了解椭圆的画法,理解椭圆的定义及焦点、焦距的概念,能正确推导椭圆的标准方程;⑵ 能够运用推导的标准方程和对椭圆的定义的理解直接写出椭圆方程过程与方法⑴ 通过对椭圆方程的推导,培养学生在解析几何中对烦琐问题运算能力,通过培养学生在解题过程中的化繁为简、化零为整的思维方法;⑵ 培养学生运动变化的观点,训练学生的动手能力;⑶ 通过作图,推导标准方程,培养学生发现问题、分析问题、解决问题的能力情感、态度与价值观⑴ 通过小组合作,培养学生的协作、互助精神;⑵ 感受椭圆曲线美,体验数学中形数互化,获得数形中的辨证思想,形成思标维的发散与集中,体验在解题过程中感悟探索的快乐与满足,增强学习兴趣教学重点椭圆的定义和椭圆的标准方程教学难点椭圆标准方程的推导教学方法小组合作探究的方法教学手段多媒体计算机教 学 过 程教师活动与学生活动设计意图1.【情景设置】提出问题:中国神州 6 号飞船发射成功,顺利进入预定轨道运行。请问:神州 6 号飞船绕什么旋转?运行轨迹是什么?(地球、椭圆)生活中你还见过椭圆形状的物品?请举例说明。教师提出课题:椭圆的定义及其标准方程2.【几何画板演示】动画演示,并同时显示,当点运动时,的数值,可知点在运动时,在改变,而的值却始终不变。教师再次演示,并提出问题,演示过程中,哪些量在变,哪些量不变?教师顺势提出椭圆应如何定义?学生思考后,教师组织学生讨论,给出定义3.【小组合作,画图探究,形成概念】小组合作后得出:椭圆是到两个定点的距离之和为常数的点的轨迹。设教师布置:下面大家自己动手画椭圆,看刚才所给的定义还有没有其他限制条件?让学生拿出课前准备好的纸板、细绳、两枚图钉,2 人一组按课本上要求画椭圆,并讨论以下问题:⑴ 在纸板上作图说明了什么?⑵ 在绳长不变的条件下,改变两个图钉之间的距离,画出的椭圆有何变化?当两个图钉重合在一起,画出的图形是什么?当两个图钉之间的距离等于绳长时,画出的图形是什么?当两个图钉固定,能使绳长小于两图钉之间的距离吗?能画出图形吗?⑶ 完善椭圆定义学生:独立思考→小组讨论→互为补充→共同交流教师:启发诱导→点拨释疑→激励完善演示课件:展示三种不同情形轨迹,...