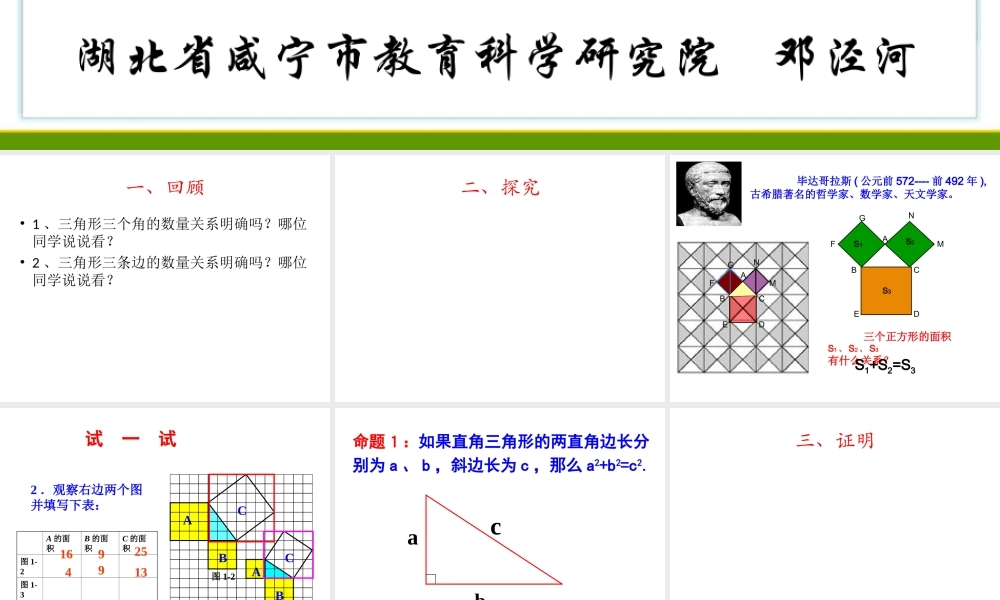
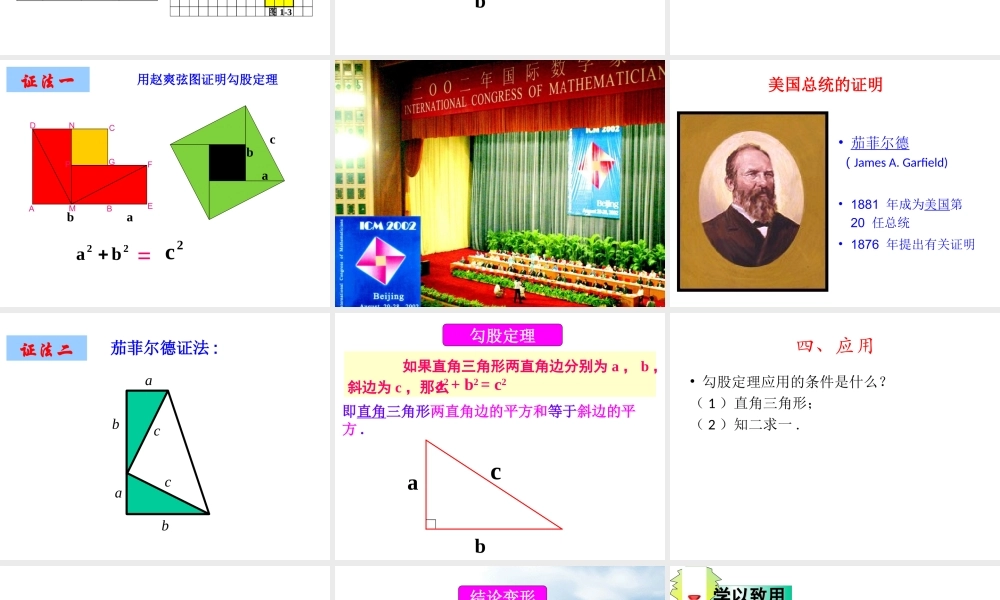
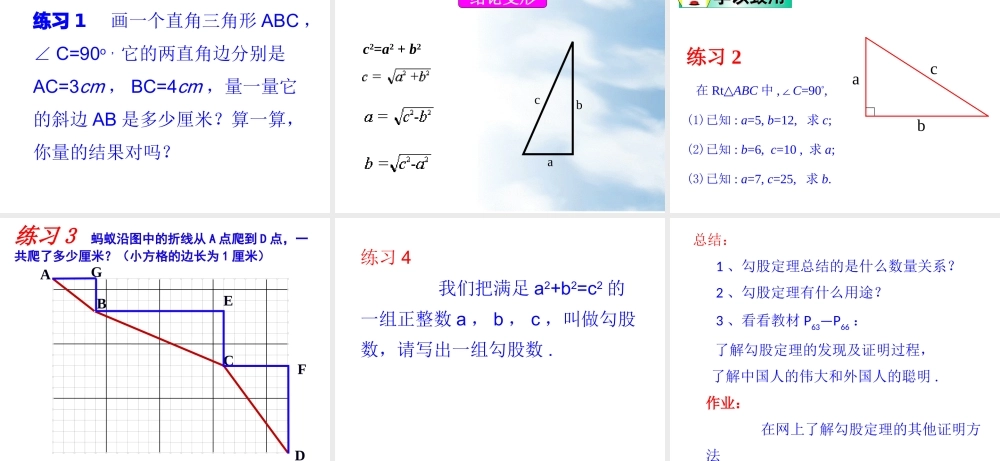
勾股定理义务教育课程标准实验教科书 八年级 下册湖北省咸宁市教育科学研究院 邓泾河一、回顾• 1 、三角形三个角的数量关系明确吗?哪位同学说说看?• 2 、三角形三条边的数量关系明确吗?哪位同学说说看?二、探究 毕达哥拉斯 ( 公元前 572---- 前 492 年 ),古希腊著名的哲学家、数学家、天文学家。 三个正方形的面积S1 、 S2 、 S3有什么关系?S1+S2=S3ABCDEFGNMABCNMDGFES3S1S2ABC图 1-2ABC图 1-32 .观察右边两个图并填写下表:A 的面积B 的面积C 的面积图 1-2图 1-3169254913试 一 试命题1:如果直角三角形的两直角边长分别为 a 、 b ,斜边长为 c ,那么 a2+b2=c2.cab三、证明cba用赵爽弦图证明勾股定理=证法一ba22ba 2cABCDEFGMNP美国总统的证明• 茄菲尔德 ( James A. Garfield)• 1881 年成为美国第 20 任总统• 1876 年提出有关证明证法二aabbcc茄菲尔德证法 : 如果直角三角形两直角边分别为 a , b ,斜边为 c ,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方 .勾股定理cab四、应用• 勾股定理应用的条件是什么?( 1 )直角三角形;( 2 )知二求一 .练习 1 画一个直角三角形 ABC ,∠ C=90o ,它的两直角边分别是AC=3cm , BC=4cm ,量一量它的斜边 AB 是多少厘米?算一算,你量的结果对吗?abcc2=a2 + b2结论变形练习 2 在 Rt△ABC 中 ,∠C=90°,(1)已知 : a=5, b=12, 求 c;(2)已知 : b=6,c=10 , 求 a;(3)已知 : a=7, c=25, 求 b.学以致用学以致用cabDABC练习 3 蚂蚁沿图中的折线从 A 点爬到 D 点,一共爬了多少厘米?(小方格的边长为 1 厘米)GFE练习 4 我们把满足 a2+b2=c2 的一组正整数 a , b , c ,叫做勾股数,请写出一组勾股数 .总结: 1 、勾股定理总结的是什么数量关系? 2 、勾股定理有什么用途? 3 、看看教材 P63—P66 : 了解勾股定理的发现及证明过程, 了解中国人的伟大和外国人的聪明 .作业: 在网上了解勾股定理的其他证明方法