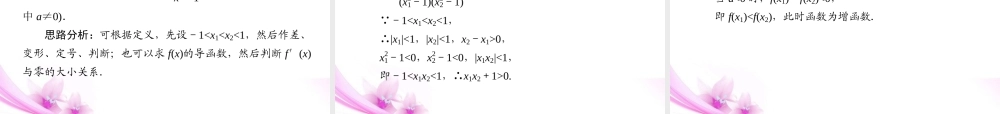考纲要求1. 理解函数的单调性、最大值、最小值及其几何意义.2 .会运用函数图象理解和研究函数的单调性 .热点提示1. 在这几年高考卷中本节内容在选择、填空、解答题中均有出现,考查的难度多为中档.2 .考查复合函数单调性常与函数的图象相结合是高考命题的热点,此类型题多出现在小题中.3 .在解答题中考查时常与导数相结合,考查函数单调性的判定或由函数的单调性确定参数问题.1 .函数的单调性(1) 单调函数的定义设函数 f(x) 的定义域为 I ,如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 x1, x2,当 x1f(x2)区间 D区间 D(2) 单调区间的定义若函数 f(x) 在区间 D 上是或,则称函数 f(x) 在这一区间上具有 ( 严格的 ) 单调性,叫做 f(x) 的单调区间.增函数减函数区间 D2 .函数的最值(1) 设函数 y = f(x) 的定义域为 I ,如果存在实数 M ,满足:① 对于任意的 x∈I ,都有;② 存在 x0∈I ,使得.则称 M 是 f(x) 的最大值.f(x)≤Mf(x0) = M(2) 设函数 y = f(x) 的定义域为 I ,如果存在实数 M ,满足:① 对于任意的 x∈I ,都有;② 存在 x0∈I ,使得.则称 M 是 f(x) 的最小值.f(x)≥Mf(x0) = M3.判断函数单调性的方法 (1)定义法:利用定义严格判断. (2)利用函数的运算性质:如若 f(x)、g(x)为增函数,则 ①f(x)+g(x)为增函数; ② 1f(x)为减函数(f(x)>0); ③ f(x)为增函数(f(x)≥0); ④f(x)·g(x)为增函数(f(x)>0,g(x)>0); ⑤-f(x)为减函数. (3) 利用复合函数关系判断单调性.“法则是”,即两个简单函数的单调性相同,则这两个函数的复合函数为,若两个简单函数的单调性相反,则这两个函数的复合函数为 .(4) 图象法.(5) 奇函数在两个对称的区间上具有的单调性;偶函数在两个对称的区间上具有的单调性.同增异减增函数减函数相同相反 (6) 导数法① 若 f(x) 在某个区间内可导,当 f′(x)>0 时, f(x) 为 函数;当 f′(x)<0 时, f(x) 为 函数;② 若 f(x) 在某个区间内可导,当 f(x) 在该区间上递增时,则 f′(x) 0 ;当 f(x) 在该区间上递减时,则 f′(x)0.( 且 f′(x) = 0 处是几个孤立点 )增减≥≤ 1 .已知函数 y = f(x) 是定义在 R 上的增函数,则 f(x) = 0 ...