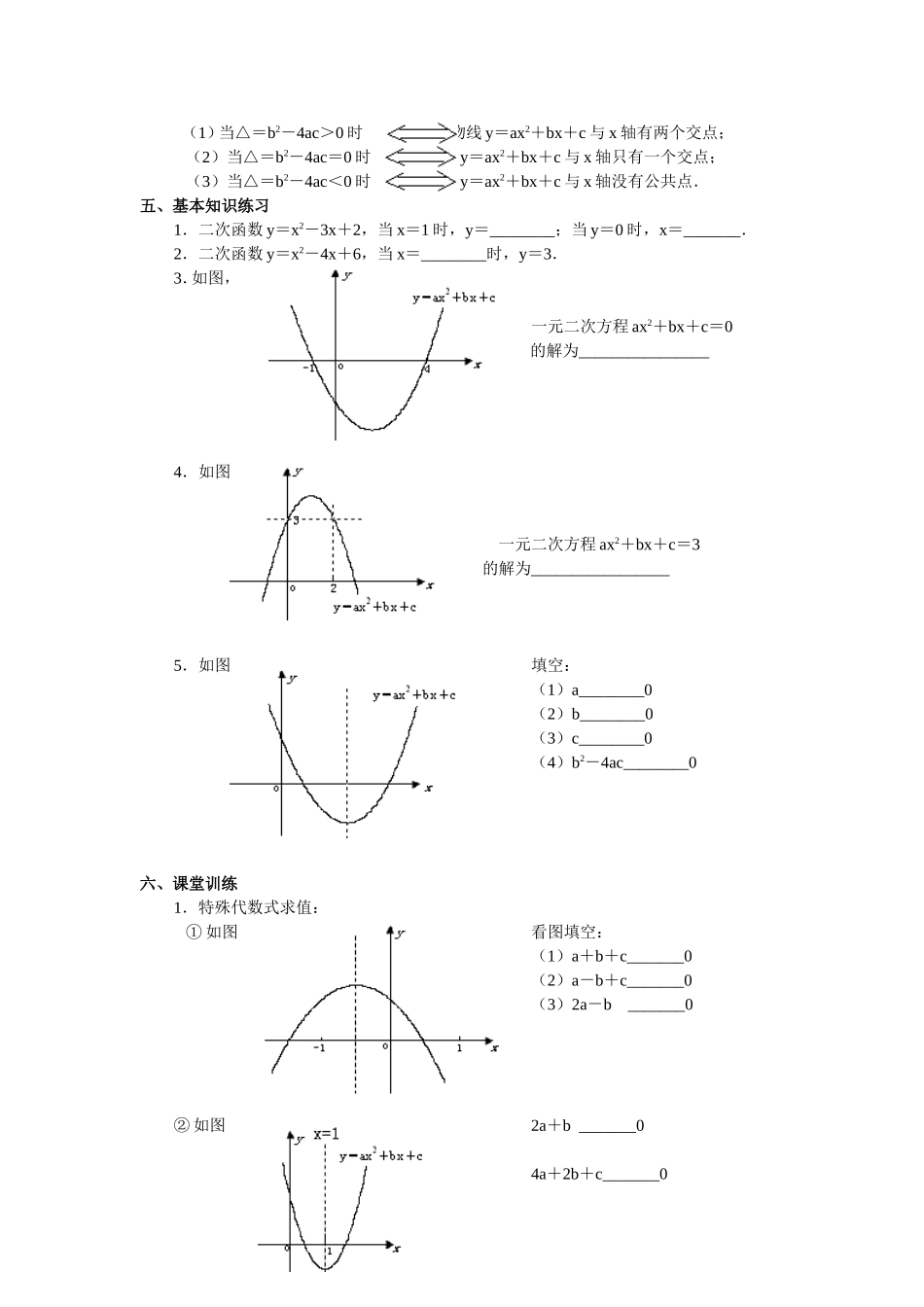
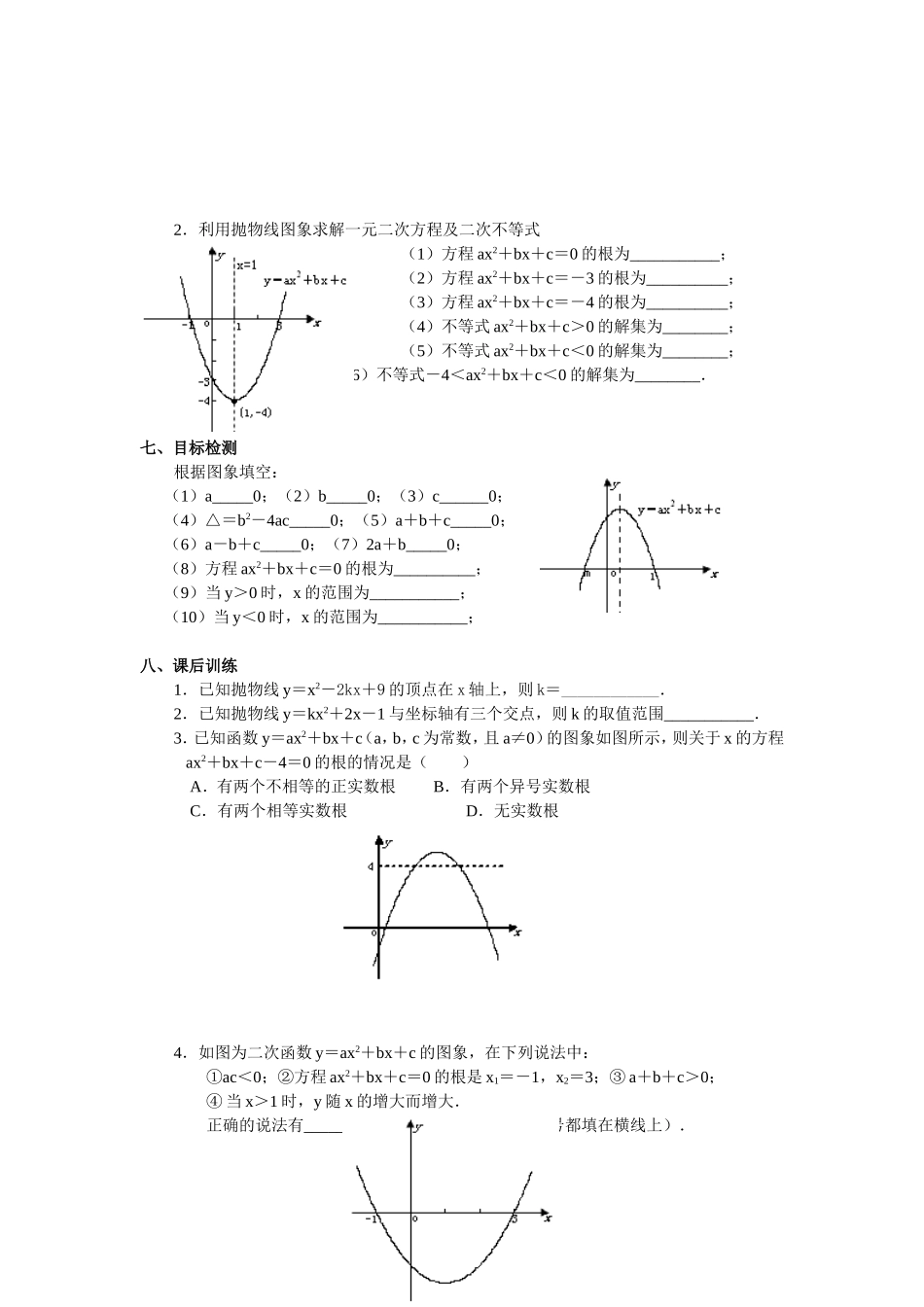
第 10 课时 用函数观点看一元二次方程一、阅读课本:第 20~22 页二、学习目标:1.知道二次函数与一元二次方程的关系.2.会用一元二次方程 ax2+bx+c=0 根的判别式△=b2-4ac 判断二次函数 y=ax2+bx+c 与 x 轴的公共点的个数.三、探索新知1.问题:如图,以 40m/s 的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度 h(单位:m)与飞行时间 t(单位:s)之间具有关系 h=20t-5t2. 考虑以下问题: (1)球的飞行高度能否达到 15m?如能,需要多少飞行时间? (2)球的飞行高度能否达到 20m?如能,需要多少飞行时间? (3)球的飞行高度能否达到 20.5m?为什么? (4)球从飞出到落地要用多少时间?2.观察图象: (1)二次函数 y=x2+x-2 的图象与 x 轴有____个交点,则一元二次方程 x2+x-2=0的根的判别式△=_______0; (2)二次函数 y=x2-6x+9 的图像与 x 轴有___________个交点,则一元二次方程x2-6x+9=0 的根的判别式△=_______0; (3)二次函数 y=x2-x+1 的图象与 x 轴________公共点,则一元二次方程 x2-x+1=0的根的判别式△_______0.四、理一理知识1.已知二次函数 y=-x2+4x 的函数值为 3,求自变量 x 的值,可以看作解一元二次方程 __________________.反之,解一元二次方程-x2+4x=3 又可以看作已知二次函数 __________________的函数值为 3 的自变量 x 的值. 一般地:已知二次函数 y=ax2+bx+c 的函数值为 m,求自变量 x 的值,可以看作解一元二次方程 ax2+bx+c=m.反之,解一元二次方程 ax2+bx+c=m 又可以看作已知二次函数 y=ax2+bx+c 的值为 m 的自变量 x 的值.2.二次函数 y=ax2+bx+c 与 x 轴的位置关系: 一元二次方程 ax2+bx+c=0 的根的判别式△=b2-4ac. (1)当△=b2-4ac>0 时抛物线 y=ax2+bx+c 与 x 轴有两个交点; (2)当△=b2-4ac=0 时 抛物线 y=ax2+bx+c 与 x 轴只有一个交点; (3)当△=b2-4ac<0 时 抛物线 y=ax2+bx+c 与 x 轴没有公共点.五、基本知识练习1.二次函数 y=x2-3x+2,当 x=1 时,y=________;当 y=0 时,x=_______.2.二次函数 y=x2-4x+6,当 x=________时,y=3.3.如图,一元二次方程 ax2+bx+c=0的解为________________4.如图一元...