一元二次方程根与系数的关系(1)VIP免费

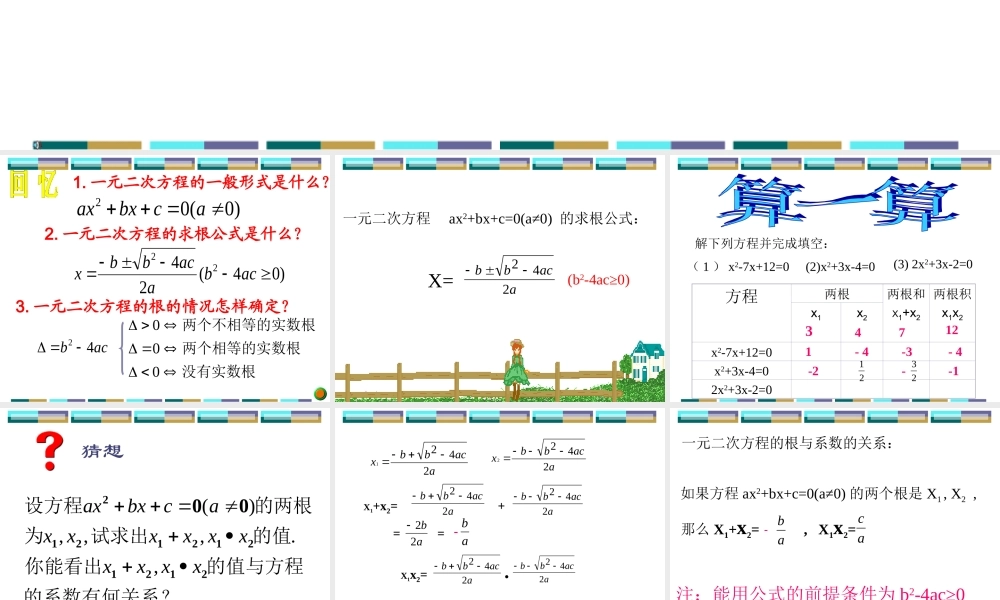
一元二次方程根与系数的关系 1. 一元二次方程的一般形式是什么？3. 一元二次方程的根的情况怎样确定？2. 一元二次方程的求根公式是什么？)0(02acbxaxacb42 没有实数根两个相等的实数根两个不相等的实数根000)04(2422acbaacbbx 一元二次方程 ax2+bx+c=0(a≠0) 的求根公式：X=aacbb242 (b2-4ac≥0) （ 1 ） x2-7x+12=0(2)x2+3x-4=0(3) 2x2+3x-2=0解下列方程并完成填空：方程两根两根和X1+x2两根积x1x2x1x2x2-7x+12=0x2+3x-4=02x2+3x-2=0341271-3- 4- 4-1--22123 的系数有何关系？的值与方程你能看出的值试求出为的两根设方程2121212121200xxxxxxxxxxacbxax,.,,,)(猜想 aacbbx2421aacbbx2422X1+x2=aacbb242 aacbb242 +=ab22=ab-X1x2=aacbb242 aacbb242 ●=242)42(2)(aacbb=244aac = ac 一元二次方程的根与系数的关系：如果方程 ax2+bx+c=0(a≠0) 的两个根是 X1 , X2 ,那么 X1+x2= , X1x2= ab-ac注：能用公式的前提条件为 b2-4ac≥0 如果方程 x2+px+q=0 的两根是X1 ， X2 ，那么 X1+X2= , X1X2=－ Pq 说出下列各方程的两根之和与两根之积：1 、 x2 - 2x - 1=02 、 2x2 - 3x + =03 、 2x2 - 6x =04 、 3x2 = 421x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2= -234134 加深理解：下列方程的两根和与两根积各是多少？ ⑴ 、 X2 － 3X+1=0 ⑵ 、 3X2 － 2X=2 ⑶ 、 2 X2+3X=-2在使用根与系数的关系时，应注意：⑴ 、不是一般式的要先化成一般式；⑵ 、在使用 X1+X2= － 时， 注意“－ ”不要漏写。（ 3 ）前提是方程有实数根即 Δ≥0 例 1 、已知方程 x2-(k+1)x+3k=0 的一个根是 2 , 求它的另一个根及 k 的值。解法一：设方程的另一个根为 x1.由根与系数的关系，得x1 ＋ 2= k+1x1 ●2= 3k解这方程组，得x1 = － 3 k = － 2答：方程的另一个根是－ 3 , k 的值是－ 2 。 例 1 、已知方程 x2-(k+1)x+3k=0 的一个根是 2 , 求它的另一个根及 k 的值。解法二：设方程的另一个根为 x1.把 x=2 代入方程，得 4-2(k+1)+3k=0解这方程，得 k= - 2由根与系数的关系，得 x1●2 ＝ 3k即 2 x1 ＝－ 6 ∴ x1 ＝－ 3答：方程的另一个根是－ 3 , k 的值是－ 2 。 1 、已知方程...