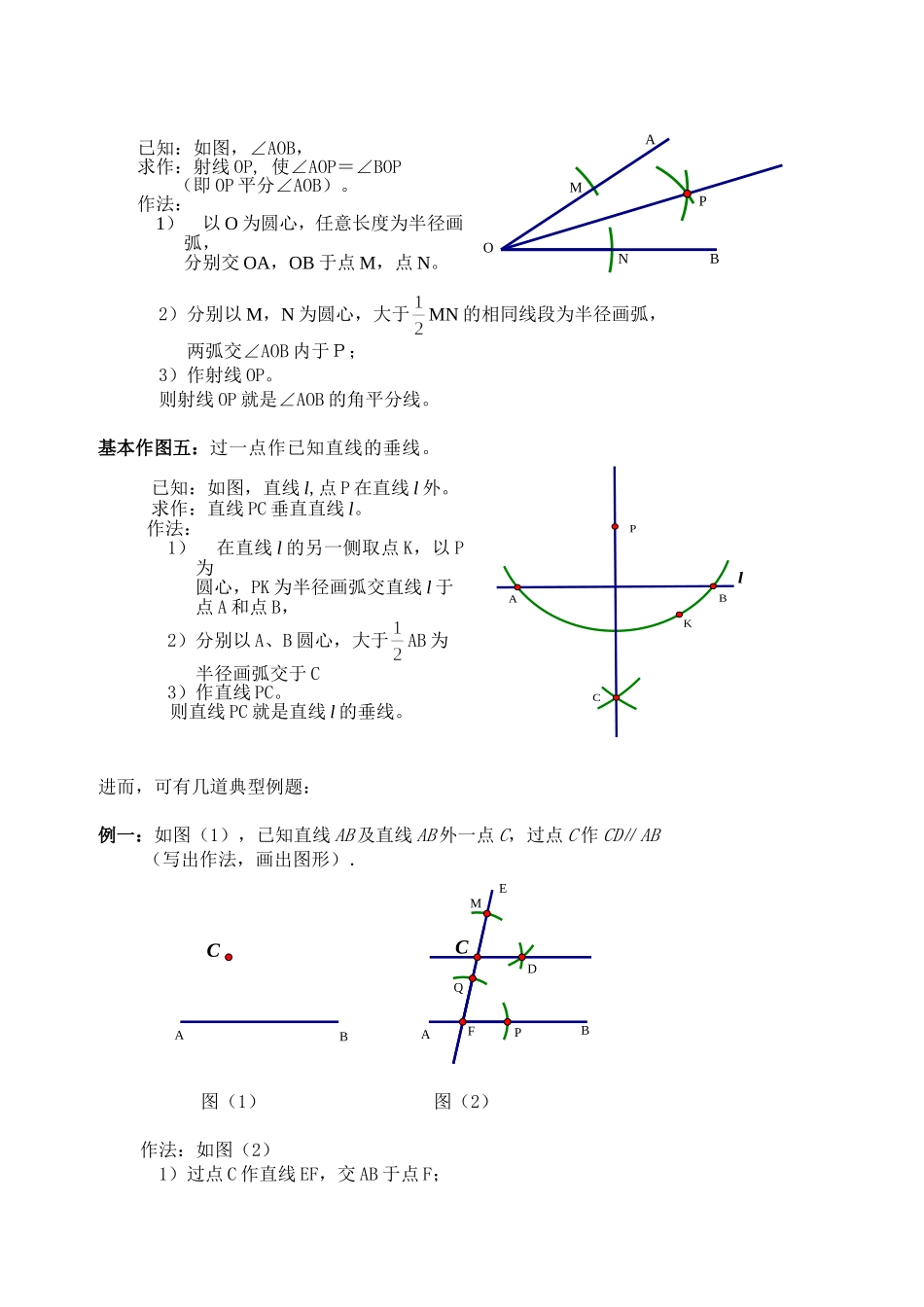
分析初中尺规作图题什么叫做尺规作图呢?尺规作图是起源于古希腊的数学课题,是指用没有刻度的直尺和圆规作图。其中直尺必须没有刻度,只能用来作直线、线段、射线或延长线段;圆规可以开至无限宽,但上面也不能有刻度,只能用来作圆和圆弧.因此,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不可以度量的.针对初中阶段学习的尺规作图题,首先,我们应该熟悉掌握该题型的规范用语:第一:用直尺作图的几何语言有三种,分别为:①过点×、点×作直线××;或作直线××;或作射线××;②过两点××做线段××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;第二:用圆规作图的几何语言可总结为四种,分别为:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×.其次,我们需要掌握尺规作图题的一些方法步骤:①当发现作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;②能根据题目可以画出要求作出的图形,以及可以列出该图形应满足的条件有哪些;③能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般会保留作图痕迹.应该注意的是,对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在许多中考作图题中,我们会发现,尺规作图题很多都是只要求保留作图痕迹,不需要写出作法,由此可见,在解作图题时,保留作图痕迹是非常重要的。当然,在初中阶段,我们常考的不是简单的尺规作图题,而是复杂的尺规作图题。而复杂的尺规作图都是由基本作图组成的,那么最常用的基本作图一共有五种,分别为:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线;我们只有掌握了尺规作图的这五种基本作图,才能更好地挑战复杂的尺规作图题。下面,我将对这五种基本作图一一阐述:基本作图一:作一条线段等于已知线段。PaBaA基本作图二:作一个角等于已知角。R图(2)图(1)QDCPNBMAO已知:如图(1),∠NOM。求作:某个角等于∠NOM。作法:如图(2),1)作射线PQ;2)在图(1)上,以O为圆心,任意长为半径作弧,交OM于点A,交ON于点B;3)以P为圆心,OA的长为半径作弧,交PQ于点C;4)以C为圆心,以AB的长为半径作弧,交前弧于点D;5)过点D作射线PR.则∠CPD就是所要求作的角.基本作图三:作已知线段的垂直平分线。DCAB基本作图四:作已知角的角平分线。已知:如图,线段a.求作:线段AB,使AB=a.作法:1)作射线AP;2)在射线AP上截取AB=a.则线段AB就是所求作的图形。已已知:线段AB求作:线段AB的垂直平分线。作法:1)以A为圆心,取比线段AB长的长度为半径在线段AB的上方和下方作弧。2)以B为圆心,取与1)等长的半径,在线段AB的上方和下方作弧,与1)作的弧分别交于点C和点D。3)过点C和点D作直线CD。则直线CD就是所要求作的垂直平分线.BAPMNO2)分别以M,N为圆心,大于MN的相同线段为半径画弧,两弧交∠AOB内于P;3)作射线OP。则射线OP就是∠AOB的角平分线。基本作图五:过一点作已知直线的垂线。lCKPBA进而,可有几道典型例题:例一:如图(1),已知直线AB及直线AB外一点C,过点C作CD∥AB(写出作法,画出图形).EMQPFDBABACC图(1)图(2)作法:如图(2)1)过点C作直线EF,交AB于点F;已知:如图,∠AOB,求作:射线OP,使∠AOP=∠BOP(即OP平分∠AOB)。作法:1)以O为圆心,任意长度为半径画弧,分别交OA,OB于点M,点N。已知:如图,直线l,点P在直线l外。求作:直线PC垂直直线l。作法:1)在直线l的另一侧取点K,以P为圆心,PK为半径画弧交直线l于点A和点B,2)分别以A、B圆心,大于AB为半径画弧交于C3)作直线PC。则直线PC就是直线l的垂线。2)以点F为圆心,以任意长为半径作弧,交FB于点P,交EF于点Q;3)以点C为圆心,...