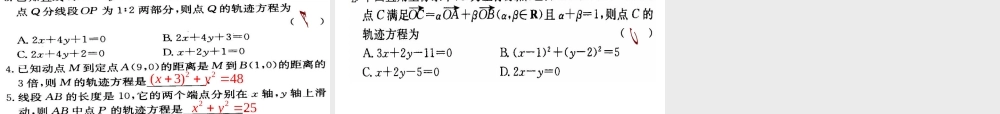求曲线的方程VIP免费

2.1.22.1.2 求曲线的方程求曲线的方程复习回顾复习回顾复习回顾复习回顾2. 练习：(1) 设 A(2,0) 、 B(0,2) ， 能否说线段 AB 的方程为 x+y-2=0? (2) 方程 x2-y2=0 表示的图形是 _______1. 复习曲线的方程和方程的曲线的概念3. 证明已知曲线的方程的方法和步骤 第一步，设 M (x0,y0) 是曲线 C 上任一点，证明 (x0,y0) 是 f(x,y)=0 的解； 证明已知曲线的方程的方法和步骤 第二步，设 (x0,y0) 是 f(x,y)=0 的解，证明点 M (x0,y0) 在曲线 C 上 . 上一节，我们已经建立了曲线的方程 . 方程的曲线的概念 . 利用这两个重要概念，就可以借助于坐标系，用坐标表示点，把曲线看成满足某种条件的点的集合或轨迹，用曲线上点的坐标（ x,y ）所满足的方程 f(x,y)=0 表示曲线，通过研究方程的性质间接地来研究曲线的性质 . 这一节，我们就来学习这一方法 .M点, )x y坐标(按某中规律运动C曲线,x y的制约条件( , )0f x y 方程几何意义代数意义“ 数形结合” 数学思想的基础1 ．解析几何与坐标法：我们把借助于坐标系研究几何图形的方法叫做坐标法 . 在数学中，用坐标法研究几何图形的知识形成了一门叫解析几何的学科 . 因此，解析几何是用代数方法研究几何问题的一门数学学科 .2 ．平面解析几何研究的主要问题：（ 1 ）根据已知条件，求出表示平面曲线的方程； （ 2 ）通过方程，研究平面曲线的性质 .说明：本节主要讨论求解曲线方程的一般步骤 .|||| MBMAMP2222)7()3()1()1(yxyx.由两点间的距离公式，点 M 所适合条件可表示为：将上式两边平方，整理得： x+2y － 7=0 ①我们证明方程①是线段 AB 的垂直平分线的方程 .（ 1 ）由求方程的过程可知，垂直平分线上每一点的坐标都是方程①解；（ 2 ）设点 M1 的坐标（ x1,y1 ）是方程①的解，即 : x+2y1 － 7=0 x1=7 － 2y1解 : 如图，设 M(x,y) 是线段 AB 的垂直平分线上任意一点 , 也就是点 M 属于集合例 2. 设 A 、 B 两点的坐标是 ( － 1, － 1) ，(3,7) ，求线段 AB 的垂直平分线的方程 .;)136(5 )1()28( )1()1(121212121211yyyyyxAM,)136(5 )7()24( )7()3(11121212121211BMAMyyyyyxBM即点 M1 在线段 AB 的垂直平分线上 .由 (1) 、 (2) 可知方程①是线段 AB 的垂直平分线的方程 .点...