高三数学月考、联考、模拟考试卷汇编 空间向量在立体几何中的应用考试卷VIP免费

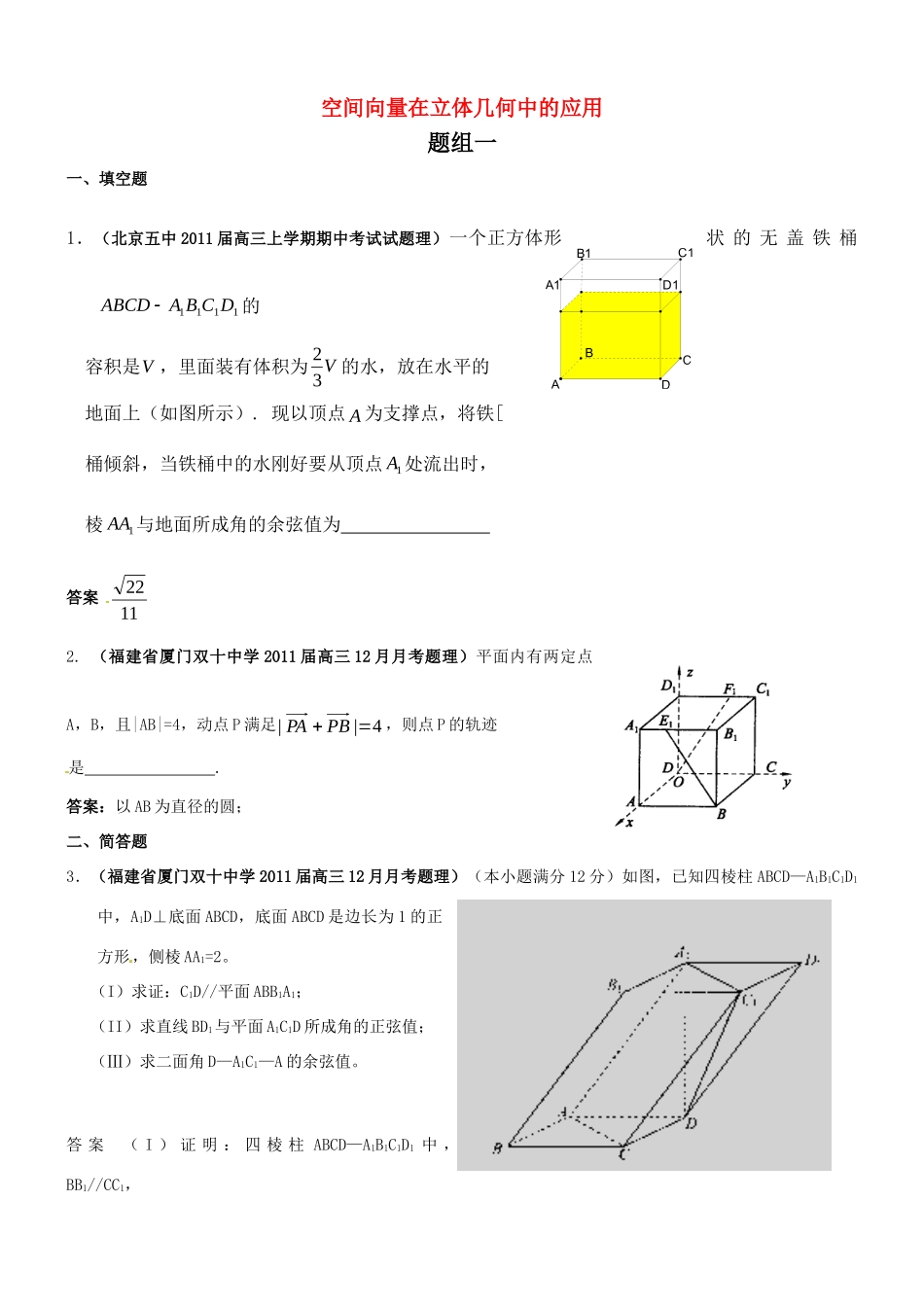
D1A1DAB1C1CB空间向量在立体几何中的应用题组一一、填空题 1．（北京五中 2011 届高三上学期期中考试试题理）一个正方体形状 的 无 盖 铁 桶1111DCBAABCD 的容积是V ，里面装有体积为V32的水，放在水平的地面上（如图所示）. 现以顶点 A 为支撑点，将铁[ 桶倾斜，当铁桶中的水刚好要从顶点1A 处流出时，棱1AA 与地面所成角的余弦值为 答案 11222. （福建省厦门双十中学 2011 届高三 12 月月考题理）平面内有两定点A，B，且|AB|=4，动点 P 满足4|| PBPA，则点 P 的轨迹是 .答案：以 AB 为直径的圆；二、简答题3．（福建省厦门双十中学 2011 届高三 12 月月考题理）（本小题满分 12 分）如图，已知四棱柱 ABCD—A1B1C1D1中，A1D⊥底面 ABCD，底面 ABCD 是边长为 1 的正方形，侧棱 AA1=2。 （I）求证：C1D//平面 ABB1A1； （II）求直线 BD1与平面 A1C1D 所成角的正弦值； （Ⅲ）求二面角 D—A1C1—A 的余弦值。 答 案 （ I ） 证 明 ： 四 棱 柱 ABCD—A1B1C1D1 中 ，BB1//CC1，又1CC面 ABB1A1，所以 CC1//平面 ABB1A1，…………2 分ABCD 是正方形，所以 CD//AB，又 CD面 ABB1A1，AB面 ABB1A1，所以 CD//平面 ABB1A1，…………3 分所以平面 CDD1C1//平面 ABB1A1，所以 C1D//平面 ABB1A1…………4 分 （II）解：ABCD 是正方形，AD⊥CD因为 A1D⊥平面 ABCD，所以 A1D⊥AD，A1D⊥CD，如图，以 D 为原点建立空间直角坐标系 D—xyz，…………5 分在1ADA中，由已知可得,31DA所以)3,1,1(),0,0,1(),3,0,0(),0,0,0(11CAAD，),0,1,1(),3,0,1(),3,1,0(11BDB),3,1,2(1BD …………6 分因为 A1D⊥平面 ABCD，所以 A1D⊥平面 A1B1C1D1A1D⊥B1D1。又 B1D1⊥A1C1，所以 B1D1⊥平面 A1C1D，…………7 分所以平面 A1C1D 的一个法向量为 n=（1，1，0）…………8 分设1BD 与 n 所成的角为  ，则,43823||||cos11BDnBDn所以直线 BD1与平面 A1C1D 所成角的正弦值为.43…………9 分 （III）解：平面 A1C1A 的法向量为),,(cbam  则,0,0111AAmCAm 所以03,0caba 令,3c可得)3,3,3(m …………11 分则.7422126||||,cosnmnmnm所以二面角ACAD11的余弦值为.742…………12 分4．（北京五中 2011 届高三上学期期中考试试题理）如图①，正三角形 ABC 边长 2，CD...